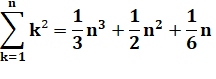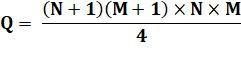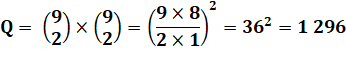|
|||||||||||||||||||||||||||||||||||||||||||
![]()
|
Hannibal,
le jour de la bataille de Zama, n'avait pas pu gagner une seule partie
d'échecs parce qu'il avait toujours eu Scipion
devant lui. Marquis de Bièvre |
Voir Pensées & humour/ Alphabet parlant
|
ÉCHECS – Introduction & Invention Au-delà du jeu classique, le
jeu d'échecs se prête à de nombreux puzzles ou
curiosités, comme l'indépendance des reines ou
l'indépendance des tours. |
|
|
||||||||||||||
|
|
|
|||||||||||||
Mouvement
des pièces

Le A renversé veut dire quelconque
|
Si le roi est la seule pièce qui peut
encore jouer, et s'il ne peut plus avancer sans être mis en échec, alors
c'est une partie nulle dite pat. |
Voir Pensées & humour
|
|
|||||||||
|
Français |
Ancien
fr |
Anglais |
Allemand |
Espagnol |
Italien
|
Latin |
Sanskrit |
Persan |
Arabe |
|
Échecs |
Esches |
Chess |
das Schach (spiel) |
Ajedres |
Scacchi |
Scaci, Ludus scacorum |
Chaturanga |
Chatrang |
Shatranj |
|
Roi |
Roy |
King |
König |
Rey |
Re |
Rex (scacum) |
Rajah |
Shah |
Shah |
|
Dame |
Fierge |
Queen |
Dame Königin |
Dama Reina |
Donna Regina |
Ferzia |
Mantri |
Farzin |
Firzan, Fiz (Vizir) |
|
Fou |
Roc |
Bishop |
Läufer |
Alfil |
Alfiere |
Rochus |
Roka (bateau) |
Rukh |
Rukh |
|
Cavalier |
Chevalier |
Knight |
Springer |
Caballo |
Cavallo |
Equus |
Ashwa |
Asp |
Faras |
|
Tour |
Alphin, Aufin |
Rook |
Turm |
Torre |
Torre |
Alphiles |
Hasti |
Pil |
Fil |
|
Pion |
Paon |
Pawn |
Bauer |
Peon |
Pedone |
Pedes |
Padati |
Piyadah |
Baidaq |
|
|
||
|
Le système de classement des
joueurs d'échecs(FIDE) a été mis au point par le physicien américain
d'origine hongroise Arpad Elo. |
||
|
1000 à 2000 |
Débutant à très bon joueur. |
|
|
2000 à 2500 |
Niveau national et international. |
|
|
2500 à 2800 |
La quelques centaines des meilleurs mondiaux. |
|
|
> 2800 |
Les six qui ont dépassé ce niveau: Kasparov (2860),
Anand, Kramnik, Topalov, Aronian, Carlsen |
|
|
|
||
|
=
264 – 1
|
||
|
264 – 1 = |
1,8 1019 18 446 744 073 709 551 615 193 707 721 x 761 838 257 287 |
|
Voir Nombres
voisins
|
relative
à l'invention des échecs |
|
|
|
|
Voir Tour de Brahmâ / Humour 2011
|
|
|||||||||||||||||
|
|
|||||||||||||||||
Beaumarchais serait mort en jouant aux échecs
|
Ce
soir là, Beaumarchais (1732-1799), dit l'anecdote, jouait aux échecs (en vérité,
il s'agissait des dames) avec le libraire Bossange. La partie durait et le
valet signala qu'il était temps d'aller au lit. Beaumarchais se coucha
sagement et mourut quelques heures après. |
L'incroyable sort de Yusuf (XIVe siècle)
|
Yusuf est enfermé dans un cachot depuis douze ans, quand une
grave maladie terrassa le roi Mahmoud. Il faut dire que Yusuf, l'ainé, avait
été détrôné par son frère cadet Mahmoud. Mahmoud avant d'expirer, donne l'ordre d'égorger Yusuf, sans
quoi il va revenir au pouvoir au détriment de ses propres fils. Les janissaires chargés de l'exécution se présentent à la
forteresse et trouvent Ysuf faisant une partie d'échecs avec le gouverneur. Comprenant la situation, Yusuf plaide pour attendre la fin
de la partie Compréhensifs envers une personnalité de cette noblesse, les
janissaires acceptent. La partie dure sept heures encore. Juste au moment de prononcer le fameux "échecs et
mat", de grands cris retentissent dans la cour centrale: Mahmoud est
mort ! Yusuf retrouve son trône et les fils de Mahmoud lui font
allégeance. Selon
l'historien espagnol Condé – La domination des Arabes en Espagne |
|
|
||||||||
|
Question Sur un plateau de 8 x 8 = 64
cases, combien peut-on dénombrer de carrés de toutes tailles? Exemple
d'un carré 3x3
|
Réponse
|
|||||||
|
Généralisation à un plateau de n×n Somme
des carrés des nombres de 1 à n |
|
|||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Question Sur un plateau de 8 x 8 = 64
cases, combien peut-on dénombrer de rectangles
de toutes tailles? Réponse:
trois méthodes 1)
Méthode directe par dénombrement Chaque case blanche indique la quantité de rectangles
de taille n x m Avec p, on indique le nombre de possibilités pour cette
dimension. On reconnait une table de
multiplication.
Sur un échiquier de 8x8, on dénombre 1 296 rectangles
de toutes tailles. Sur la diagonale (en rouge), ceux qui sont des carrés. 2)
Méthode astucieuse par comptage par les diagonales Un rectangle sur l'échiquier est entièrement défini par
une de des deux diagonales, de bas en
haut comme de haut en bas; soit quatre possibilités de diagonales pour un
rectangle. Une diagonale part d'un des 9 x 9 sommets et elle
rejoint l'un des autres, sauf ceux sur la même horizontale ou la même
verticale; restent 8x 8 arrivées. Bilan sur la quantité de rectangles: Q = ¼ x 9x9 x 8x8
= 1 296 De sorte que la généralisation à un plateau de N x M cases:
3)
Méthode mathématique par calcul des combinaisons pour l'échiquier Pour créer un rectangle, il faut choisir
2 sommets parmi 9 disponibles en horizontal et même chose ne vertical
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Combien
de triangles équilatéraux, d'hexagones
? |
|
|
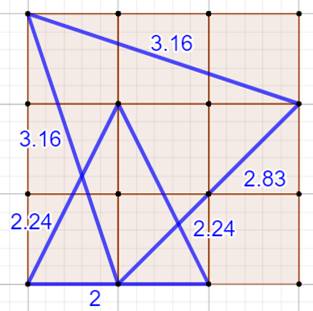
Théorème
des quinconces (E. Lucas) Les centres de trois cases
quelconques d'un échiquier de grandeur quelconque ne sont jamais situés aux
sommets d'un triangle
équilatéral ou d'un hexagone
régulier. Pourquoi
? Cette équation diophantienne n'a pas de
solution (par définition en nombres entiers): x² + y² = u² + v² = 2(ux + vy)
Isocèle,
oui; équilatéral, non.
|
|
Voir Triangles
rectangles sur grille / Carrés sur
grilles
Historique des tricheries aux échecs
|
1769 |
Wolfgang von Kempelen, ingénieur hongrois, crée le turc mécanique, u automate capable de jouer aux échecs. En réalité un joueur caché actionnait le jeu. |
|
1962 |
Bobby
Fisher, joueur américain, accuse trois joueurs soviétiques d'avoir arrangé
des parties nulles lors d'u tournoi. |
|
2006 |
Veselin
Topalov, bulgare, accuse son adversaire Vladimir Kramnik de se rendre trop
souvent aux toilettes pour tricher. |
|
2010 |
Trois
joueurs de la FFE sont accusés de triche. Par ses déplacements dans la salle,
Arnaud Hauchard transmettait à Sébastien Feller les coups calculés sur un
ordinateur par un complice. |
|
2019 |
Le
grand maitre letton Igor Tausis est surpris avec son téléphone dans les
toilettes lors de l'Open de Strasbourg. Il reconnait avoir triché. |
|
2020 |
La
FFE et la Fide mettent en place un règlement pour lutter contre la fraude en
ligne. Il est prévu qu'il soit adapté au fur et à mesure des nouvelles
techniques qui apparaitront. Notamment l'intelligence
artificielle (IA). |
|
2022 |
Magnus
Carlsen contre Hans Niemann s'incline au bout de quatre et demi de match. Il
l'accuse d'avoir triché. Certains
constatent qu'il ne regarde pas beaucoup l'échiquier et pourtant trouve les
bons coups rapidement. Suspect ! D'autant que Niemann avait confessé avoir
triché lors d'une centaine de parties précédentes. En fait, en l'occurrence, difficile
de le prouver. On
a imaginé la présence d'un minuscule appareil qui serait passé à travers les
contrôles |
|
Actualités |
Les
méthodes de détection de fraudes actuelles essaient de détecter une réaction
humaine d'une initiative par ordinateur. L'un estime le gain
"immédiat", l'autre le chemin pour aboutir au mat. Un
autre contrôle consiste à évaluer le coup du joueur en fonction de ce qui est
probable pour son niveau. |
|
Méthodes |
Les
calculs reposent sur les probabilités et les méthodes bayésiennes,
c'est-à-dire sur la probabilité d'occurrence d'un événement compte tenu de ce
qui précède. |
Source: Science et Vie Janvier 2023 - N°1264
Le Turc de von Kempelen

![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()