carré parfait - pavage du carré par des carrés

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 09/01/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Topologie
Débutants Général	PAVAGE				Glossaire Topologie
INDEX Géométrie Puzzles	Approche	Avec polygones	Apériodique	Pavage fini
	Triangles	Carrés parfaits	Rectangles	Penrose (losanges)
	Pentagone	Hexagone	Dodécagone	Disque (Pizza)
	Dominos	Échiquier	Plus Plus (Jeu)
	Empilement de carrés dans un carré
		Sommaire de cette page >>> Approche >>> Le coffre de Dudeney >>> Les types de quadrature >>> Carre parfait >>> Carre composé >>> Rectangle >>> Presque carré parfait >>> Pavage du rectangle par des rectangles incomparables >>> Pavage du CARRÉ avec sept rectangles >>> Historique

CARRÉS PARFAITS

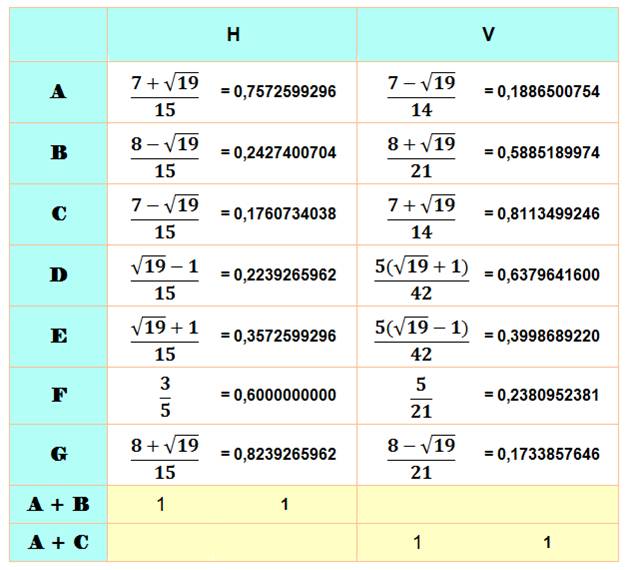
"QUADRATURE du CARRÉ"

Est-il possible de remplir un carré avec des carrés tous de taille différente?

Anglais: Tilling by squares /Tilling rectangle with rectangles / Squared squares / Squared rectangles

Devinette

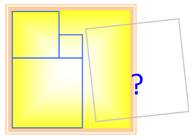
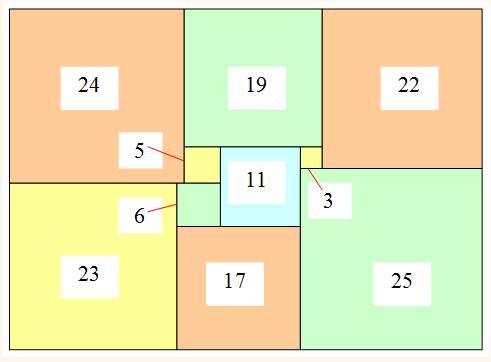
Nous souhaitons recouvrir le sol d'une pièce carrée de 4 x 4 avec de la moquette tout en respectant les carreaux. Nous disposons de ce morceau trouée

Est-ce possible? Si oui, comment minimiser la découpe.

Solution

Approche

Carré parfait

Prendre un carré et le décomposer en carrés;
Sans problème si les carrés sont identiques.

Plus difficile si on impose que tous les carrés soient différents.
C'est : la quadrature du carré ou la recherche du carré parfait.

Ordre du carré

Une quadrature est caractérisée par la taille du carré initial ainsi disséqué
et aussi, et principalement, par le nombre de carrés élémentaires nécessaires.
C'est l'ordre du carré.

Utile ou futile ?

Les carrés parfaits sont utilisés dans la théorie de Kirchhoff sur la distribution des intensités électriques dans un réseau.

Réciproquement, les lois sur les réseaux de connexion électriques ont beaucoup servi à résoudre la quadrature du carré.

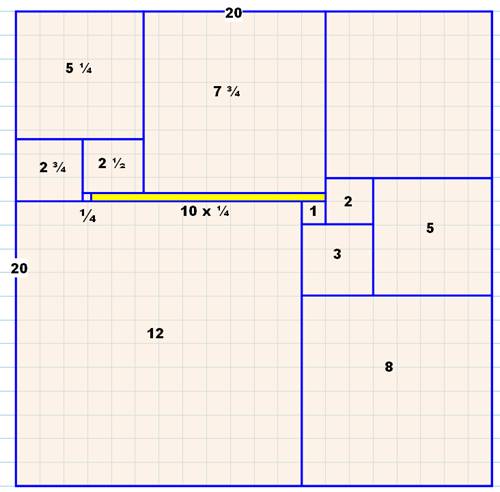
Le coffre de Dudeney – Carré presque parfait
Lady Isabel possède une coffre. Son couvercle est marqueté avec une bande dorée de 10 cm x ¼ cm et des carrés de tailles différentes telles que l'ensemble forme un grand carré. Trouvez les dimensions du couvercle.	Find the dimension of the top of the box from these facts alone: that there was a rectangular strip of gold, ten inches by ¼ inch; and the rest of the surface was exactly inlaid with pieces of wood, each piece being a perfect square, and no two pieces of the same size. The Canterbury Puzzles – Dudeney - 1910
Solution telle que donnée par Dudeney Sans en donner l'explication, Dudeney affirme que cette solution est unique. La taille finale dépend de celle de la bande dorée. Le carré n'est que presque-parfait du fait de la présence de la bande.

Les types de quadratures

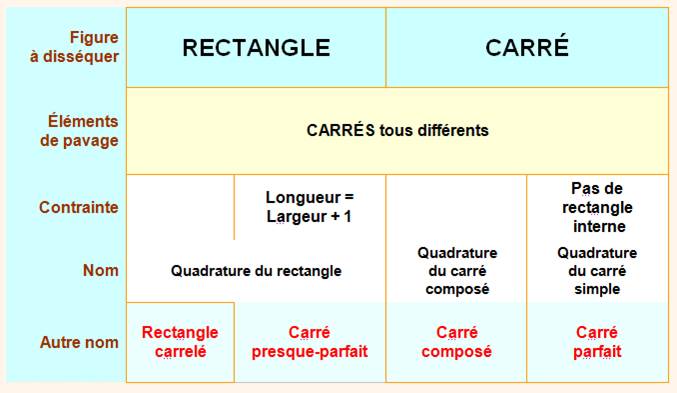
Carrés et rectangles

On peut s'intéresser aux rectangles comme aux carrés.
Il faut que tous les carrés élémentaires soient différents.

On peut ajouter une contrainte:
qu'il n'y ait pas formation de rectangles internes;
autrement dit: aucun groupe de carrés ne forme un rectangle.

Cas de quadrature

Il existe aussi le cas d'un rectangle découpé en rectangles différents.

Voir Rectangles incomparables

Records (la plus petite figure connue)

Nom

Rectangle

carrelé

Carré

presque

-parfait

Carré

composé

Carré

parfait

Ordre

Quantité

Quantité de carrés parfaits

Ordre	Composé	Simple
21	0	1
22	0	?
23	0	?
24	1	8
25	2	28
26	13	…
27	…

CARRÉ PARFAIT 112 x 112 – Ordre 21

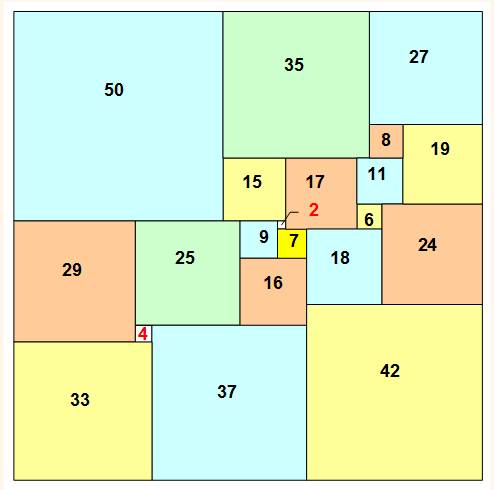
Carré formé par la somme de 21 carrés différents (aire = 112²).
Plus petit carré divisible en carrés plus petits et tous différents.
Et sans formation de rectangles internes.

Illustration

Recensement des carrés

La figure comprend 21 carrés dont voici les longueurs des côtés
2	4	6	7	8	9
11	15	16	17	18	19
24	25	27	29
33	35	37
42
50

Somme des aires

2² + 4² + 6² + 7² + 8² + 9² + 11² + 15² + 16² + 17² + 18² + 19²

+ 24² + 25² + 27² + 29² + 33² + 35² + 37² + 42² + 50²

Historique

1967 – J. C. Wilson trouve un carré parfait d'odre 25

1973 – N. D. Kazarinoff et R. Weitzenkamp montrent que l'ordre minimal est 21 ou 22.

1978 – Wilhelmus Duijvestijn (1927-1998 – Portrait ) atteint l'ordre 21 et montre que c'est le plus petit. Résultat possible du fait de la croissance de la capacité de calcul des ordinateurs.

CARRÉ COMPOSÉ 175 x 175 – Ordre 24

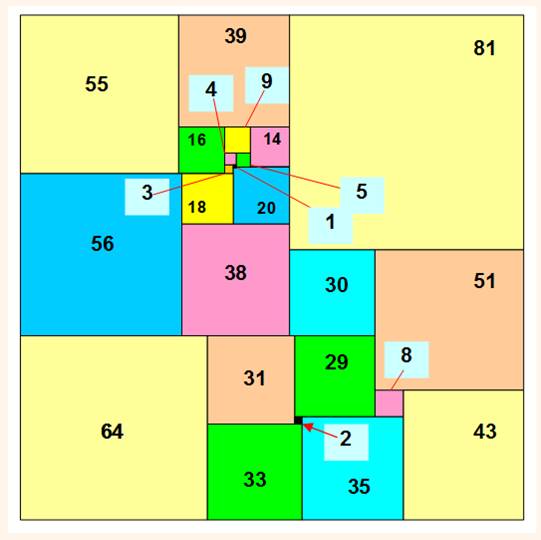
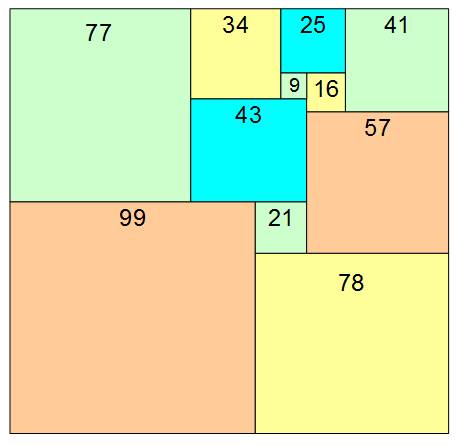
Carré formé par la somme de 24 carrés différents (aire =175²).
Plus petit carré divisible en carrés plus petits et tous différents.
Avec formation d'un rectangle interne

La figure comprend 24 carrés dont voici les longueurs des côtés
1	2	3	4	5	8	9
14	16	18
20	29
30	31	33	35	38	39
43	51	55	56
64	81

Code Bouwkamp: liste dans l'ordre de construction des carrés de gauche à droite puis de haut en bas

(24, 175, 175) (55, 39, 81, 16, 9, 14, 4, 5, 3, 1, 56, 18, 20, 38, 30, 51, 64, 31, 29, 8, 2, 33, 35, 43)

Chaque nouveau carré est placé le plus haut et le plus à gauche possible.

Variante: (24 175 175) (81 56 38 18 20 55 16 3 1 5 14 4 9 39 51 30 29 31 64 43 8 35 2 33)

Zoom autour du carré unité

RECTANGLE 32 x 33 – Ordre 9

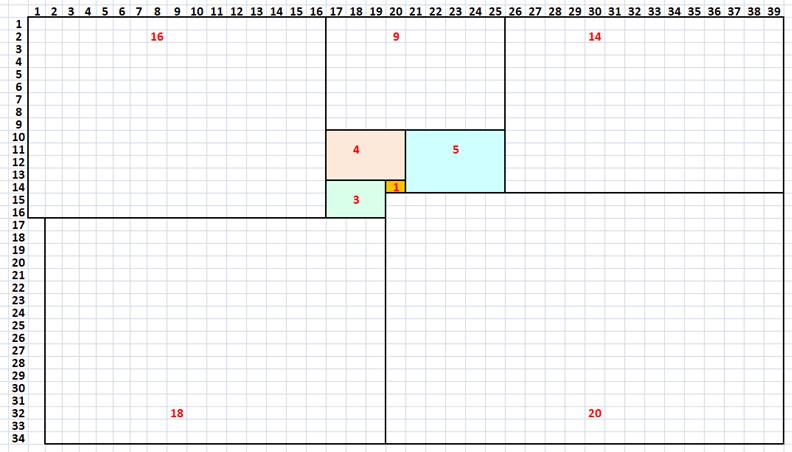
32 x 33 =>

Rectangle formé par la somme de 9 carrés différents.
Plus petit rectangle divisible en carrés plus petits et tous différents.
Sans formation d'un rectangle interne.
C'est le plus petit rectangle carrelé.
Il est aussi presque-parfait (Long = larg + 1)

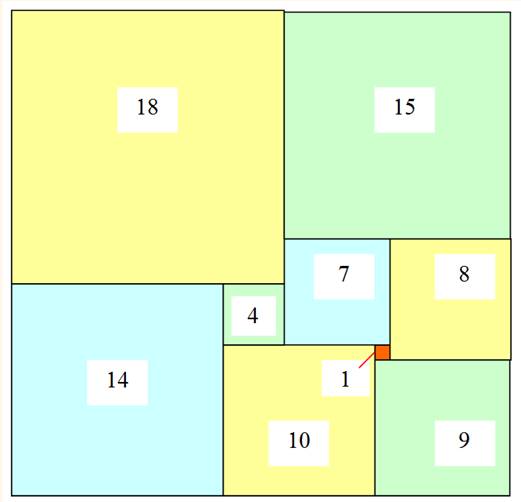
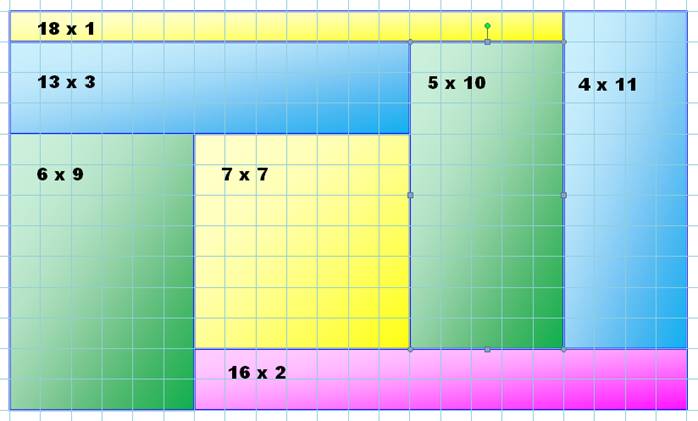
Rectangle 47 x 65 - Ordre 10

47 x 65 =>

Rectangle formé par la somme de 10 carrés différents.

Quantité de rectangles carrelés

Ordre	Composé
9	2
10	6
11	22
12	67
13	213
14	744
15	2 609
16	9 016
17	31 427
18	110 384

PRESQUE CARRÉS PARFAITS

Rectangle 32 x 33 – Ordre 9

Pavage d'un presque carré de 176 x 177 par 9 carrés. Voir ci-dessus

Rectangle 176 x 177 – Ordre 11

Pavage d'un presque carré de 176 x 177 par 11 carrés

Pavage du rectangle

par des rectangles incomparables

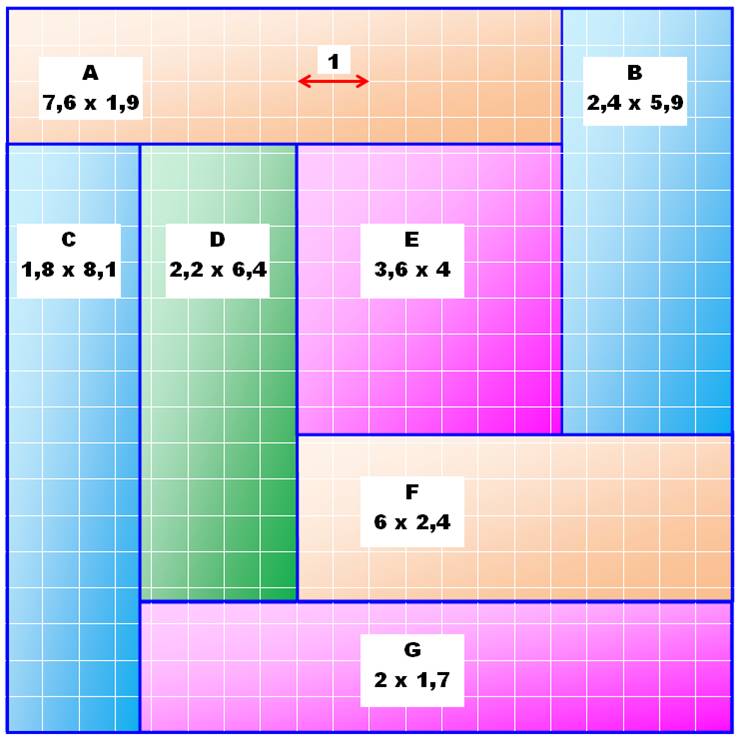
Division du rectangle en rectangles plus petits, aucun ne pouvant rentrer à l'intérieur d'un autre. Ces rectangles formant le pavage sont dits incomparables. Les rectangles, éventuellement carrés, sont disposés droits dans le rectangles initial; les côtés sont parallèles.

Le plus petit réalisable est un rectangle de 22 x 13 dont la figure montre le pavage. Notez qu'il faut sept pièces et qu'un carré 7 x 7 s'est glissé vers le centre.

Sans la contrainte d'être incomparables, il faut un minimum de sept rectangles de même aire mais de forme différente pour paver un rectangle ou un carré.

Pavage du CARRÉ avec sept rectangles

Diviser un carré en 2, engendre deux moitiés identiques.

Une découpe en 3, 4, 5 ou 6 engendrera nécessairement deux pièces identiques.

Avec un partage en sept, alors tous les rectangles peuvent être différents.

Dimensions exactes

HISTORIQUE
Année	Événements	Rectangle	Carré composé	Carré parfait
1900	Sam Lloyd – Réalise quelques quadratures mais sans la contrainte que tous les carrés soient inégaux.
1902	Dudeney propose le puzzle du coffre de Lady Isabel pour la première fois dans un magazine et repris dans le livre cité en 1910.
1925	Rectangles – Deux solutions sont publiées: 32 x 33, ordre 9 et 47 x 65, ordre 10. Le rectangle 32 x 33 a été trouvé en 1925 par Moron. Reichert et Toepkin ont prouvé en 1940 qu'il s'agissait du plus petit rectangle divisé en carrés différents.	£ 9
1930	Lusin (Moscou) conjecture que la quadrature du carré est impossible.			Impossible
1937	Vers 1937, C.A.B. Smith utilise un graphe électrique pour chercher les solutions.
1938	Université de Cambridge – Trouve une quadrature du carré d'ordre 69.			£ 69
1939	Allemagne – Une autre d'ordre 55.			£ 55
	Le plus petit rectangle carrelé est d'ordre 9 et il en existe que 2.	Min 9 Qté 2
	Le plus petit carré parfait est d'ordre supérieur à 9.			³ 10
1940	On connaît tous les rectangles carrelés jusqu'à l'ordre 13.	® 13
1948	Willcocks (Bristol GB), mathématicien amateur, trouve un carré composé d'ordre 24.		£ 24
1960	Hollande avec les ordinateurs.	® 15
1962	On continue les recherches; on est aux limites des puissances de calcul de l'époque.	® 19
1963	Nouvelle méthode dite des carrés pseudo-carrelés: 20 nouveaux carrés. On sait désormais fabriquer des carrés parfaits d'ordre élevé. Il en existe plus de 2 000 jusqu'à l'ordre 33.		25 à 29
1967	Wilson (Ontario É.-U.) utilise une méthode générale de recherche des carrés parfaits: il en trouve 5 d'ordre 25 et 24 d'ordre 26..		25, 26
	État des recherches.	® 19	24 qté 1 25 qté 2 26 qté 13	< 25 ? 25 qté 8 26 qté 28
1978	Duijvestijn (Ensched NL) utilise un programme très élaboré et explore tous les rectangles d'ordre 21. Parmi eux: un carré !	® 21		Min 21
1982	Il n'existe qu'un carré composé; c'est celui déjà trouvé d'ordre 24.		Min 24

Devinette – Solution

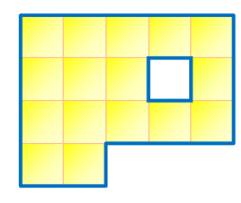
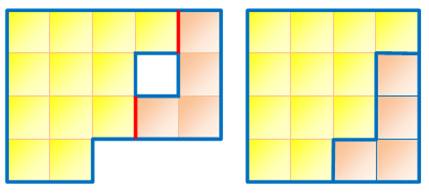
C'est faisable car la moquette comporte les 16 carrés nécessaires pour former un carré de 4 x 4. Les carreaux élémentaires ne seront pas partagés. La découpe ne nécessite que deux coups de cutter selon les lignes marquées en rouge.

Retour

Voir	Découpe du carre en 5 Empilement de carrés dans un carré Pavage avec polygones Quadrature du cercle Pentominos
Aussi	Carrés magiques Conjecture de Poincaré Dissection du carré en décagone Dissection du carré en triangles Géométrie Hilbert Jeux Pavage de l'échiquier Pavage mystérieux du triangle Rectangles incomparables Tangram
Livres	Malcolm E. Lines Ian Stewart *Martin Gardner* dans Scientific American Book of mathematical Puzzles and Diversions
Sites	Squaring the square – Wikipedia Tiling the square – Énorme! Exhaustif! Maths forum - squaring the square Chonomaths - quadrature en général To construct a square equal to a given rectilinear figure Adrianus Johannes Wilhelmus Duijvestijn (AJWD) (1927-1998) – Biography
Cette page	http://villemin.gerard.free.fr/Pavage/CarrParf.htm