|
|||||||||||||||||||||||||||||||
![]()
|
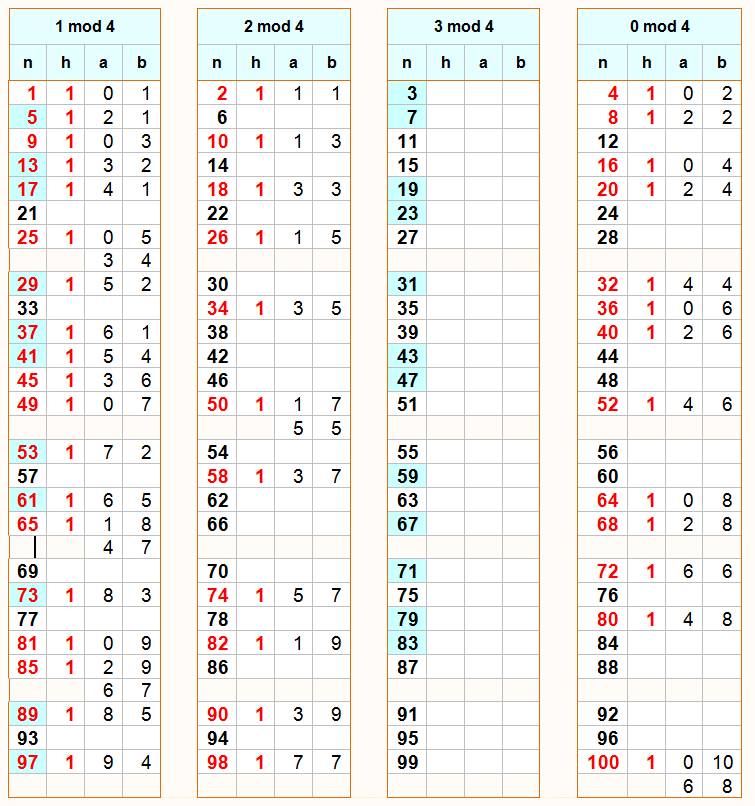
SOMME de deux CARRÉS Table des nombres de 1 à 100 Table exposée pour observation. |
|
|
|
|
Le
tableau ci-dessous donne la liste des nombres de 1 à 100:
|
|
|
|
||||||
|
Total: 43 nombres jusqu'à 100 qui sont somme
de 2 carrés (< 50%) dont 5 avec double présentation: 25, 50,
65, 85 et 100. Liste:
50, 65, 85, 125, 130, 145, 170, 185, 200, 205, 221, 250, 260, 265, 290, 305,
325, 338, 340, 365, 370, 377, 410, 425, 442, 445, 450, 481, 485, 493, 500,
505, 520, 530, 533, 545, 565, 578, 580, 585, 610, 625, 629, 650, 680, 685,
689, 697, 725, 730, 740, 745, 754, 765, …
OEIS A007692 |
||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Deux remarques immédiates
Second coup d'œil
Pour chaque nombre, on donne les termes de la somme de 2
carrés si elle existe et même chose en multipliant par 4.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/SomCaPre.htm |
![]()