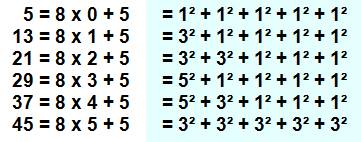|
|||||||||||||||||||||||||||||||
![]()
|
SOMME de QUATRE CARRÉS Tout
nombre est la somme de:
Généralisation
de Fermat sur les nombres
polygonaux. Voir
le récent et surprenant théorème 290. |
Voir Théorème des 15
|
Tous
les carrés sont somme de quatre carrés au moins une fois, sauf le carré de 3:
2² =
4 = 1² + 1² + 1² + 1² 3² = 9 = 1² + 2² + 2² 4² = 16 = 2² + 2² + 2² + 2² 5² = 25 = 1² + 2² + 2² + 4² 6² = 36 = 1² + 1² + 3² + 5² = 3² + 3² + 3²
+ 3² … 10² = 100 = 1² + 1²
+ 7² + 7² = 1² + 3² + 3² + 9² = 1² + 5² + 5² + 7² = 2² + 4² + 4² + 8² = 5² +
5² + 5² + 5² Les
carrés des puissances de 2
sont somme de quatre carrés une seule fois:
162
= 8² + 8² + 8² + 8² |
|
THÉORÈME
des quatre carrés de Lagrange (1770) Ou Conjecture de Bachet |
|
|
|
Tout nombre
entier est somme de quatre carrés, ou moins. Lagrange's four-square theorem Every positive integer can be represented as
the sum of four or fewer integral squares. |
Tout entier positif est représenté
par la forme quadratique: n =
a² + b² + c² + d² Voir Approche
et exemples La
démonstration dépasse le cadre de ce site. |
|
|
Avec quatre carrés exactement Tout nombre supérieur à 41 est
somme d'exactement quatre carrés non nuls. |
Nombres somme de quatre carrés non-nuls 4, 7, 10, 12, 13, 15, 16, 18, 19, 20,
21, 22, 23, 25, 26, 27, 28, 30, 31, 33, 34, 35, 36, 37, 38, 39, 40, 42, 43, 44, 45, 46, 47, 48, 49, 50, … |
|
|
Avec cinq carrés: Tout nombre supérieur à 33 est somme
d'exactement cinq carrés non nuls. |
Exemples 32 = 16 + 4 + 4 + 4 + 4 33 = 16 + 16 + 1 = 24 + 4 + 4 = 16 +
9 + 4 + 4 34 = 16 +
9 + 4 + 4 + 1 35 = 9 + 9
+ 9 + 4 + 4 … |
|
Voir Identité de Lagrange / Théorème
des 15 et théorème des 290 (formes quadratiques) /
Lagrange (1736-1813) / Bachet
de Méziriac
Premier pas pour la
démonstration du théorème
|
L'identité
des quatre
carrés d'Euler réduit la recherche aux seuls nombres premiers. Elle dit que: Le
produit de deux nombres décomposables en somme de quatre carrés est la somme
de quatre carrés: N4 x M4 = S4 |
|
|
Supposons
que tous les nombres premiers soient somme de quatre carrés (S4). |
P1
= S4 P2
= S4 |
|
Alors,
le produit de deux premiers est S4. |
P1
x P2 = S4 |
|
De
même que le produit de trois (la relation d'Euler est générale). |
P1
x P2 x P3 = S4 x P3
= S4 |
|
Tout
nombre composé est le produit de premiers. |
Composé
= S4 |
|
Reste
à démontrer que tout premier est somme de quatre carrés. Pas simple! (Le cas des nombres 1 et de 2 est
facilement vérifiable). On sait démontrer que pour tout premier, il
existe un de ses multiples qui est somme de carrés: m.p = a² + b² + c² + d² avec m inférieur à p La
démo consiste alors à montrer que le multiple m peut-être de plus en plus
petit jusqu'à égaler 1. |
|
Voir Démonstration
de Lagrange (1770) / Démonstration
façon Lagrange par Planet-Math
|
|
||
|
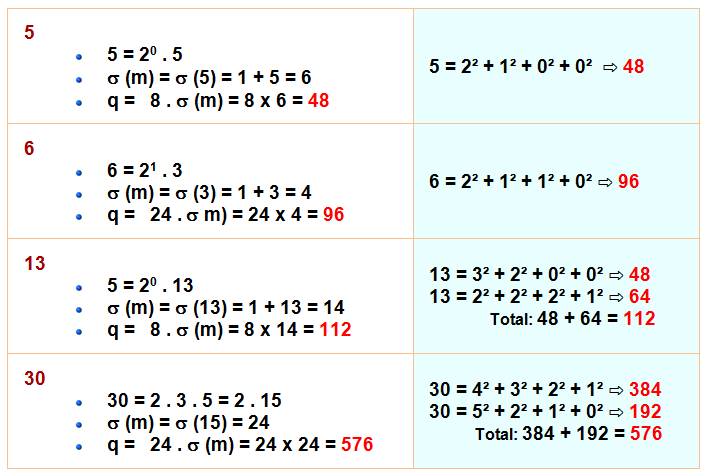
Forme canonique des nombres Pour ce théorème on utilise la forme canonique
suivante qui met en évidence les puissances de 2: Théorème de Jacobi (1829) La quantité de présentations d'un
nombre en somme de 4 carrés en tenant compte des
permutations et du signe. Sigma de m étant la somme
des diviseurs de m. |
n =
|
|
|
Façon de compter
Voir
Permutations Exemples
|
||
|
|
||
|
Théorèmes de Ramanujan – 1917 Outre la forme quadratique de
Lagrange, Ramanujan trouve cinquante-quatre autres formes quadratiques qui
représentent tous les nombres. |
Forme quadratique générale a.x2 + b.y2 + c.z2
+ d.w2 Notée: [a, b, c,
d] Cas classique de Lagrange x2 + y2 + z2
+ w2 Notée: [1, 1, 1,
1] Exemple d'une des formes de Ramanujan x2 + 2y2 + 5z2
+ 10w2 Notée: [1, 2, 5,
10] |
|
|
Les 54
formes quadratiques de Ramanujan
Il a été prouvé plus tard que ces
formes quadratiques quaternaires diagonales sont les seules possibles.
Diagonale (ou matrice diagonale)
pour exprimer le fait que ce sont des formes primitives, que les quatre
coefficients sont premiers entre eux. Évidemment ces résultats furent à
l'origine de nombreux travaux pour explorer ce sujet. Quelles formes
quadratiques représentent les entiers, les impairs, les premiers, etc? Théorème des 15 ou théorème de John Conway
et Schneeberger (1993) – Fifteen Theorem Ces deux mathématiciens prouvent un
remarquable théorème: une forme quadratique avec matrice d'entiers positifs,
représente tous les nombres positifs, si et seulement si elle les représente
jusqu'au nombre 15. Théorème des 290 ou théorème de Manjul
Bhargava et Jonathan Hanke Ce fut d'abord une conjecture émise
en 1993 par Conway et ses étudiants: Miller, Schneeberger et Simons.
Démontrée par Manjul Bhargava et Jonathan Hanke. Si une forme
quadratique à coefficients entiers représente les vingt-neuf nombres suivant,
elle les représente tous. Les 29 nombres: 1, 2, 3, 5, 6, 7,
10, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 34, 35, 37, 42, 58, 93,
110, 145, 203, et 290. |
||
Voir Srinivasa Ramanujan (1887-1920)
Suite en
Formes quadratiques et théorème
des 15 et des 290
|
|
||
|
Théorème de Minkowski (1884) Tous les nombres de la forme
indiquée sont somme de cinq carrés de nombres
impairs. |
Pour n = 8n + 5 Alors n = a² + b² + c² + d² + e² Avec: a, b, c, d, e impairs |
|
|
Exemples |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/SomCa4ca.htm
|
![]()