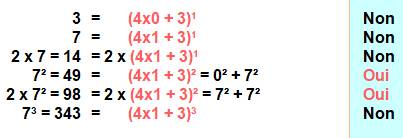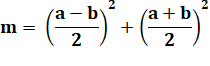|
|||||||||||||||||||||||||||||||
![]()
|
SOMME de deux CARRÉS Théorème Tout nombre premier de la forme 4n + 1 est la somme de deux carrés. |
Anglais: sum of two square
problem or Girand's problem (1627)
|
Théorème
des deux carrés de Fermat – Nombres premiers Tout
nombre PREMIER est la somme de deux carrés de façon unique si et seulement si
il est de la forme 4n + 1. Théorème
des deux carrés – Nombres quelconques Un
entier est somme de deux carrés si et seulement si chacun de ses facteurs
premiers de la forme 4k + 3 est à une puissance paire. De
plus, la décomposition est unique si aucun facteur n'est en 4k + 1, ou alors
un seul à la puissance unité. Théorème
des deux carrés de Jacobi Un
nombre entier avec K diviseurs en k + 1 et K' en 4k + 3 (diviseurs non
nécessairement premiers). Alors, la quantité Q de toutes les représentations
en somme de deux carré est égale à: Q = 4 (K + K'). |
Voir Structure des nombres
premiers
|
|
||
|
Observation
Y a-t-il anguille sous roche? Voyons quelques nombres sous cet angle.
|
||
|
Avec un terme en 4k + 3
|
|
|
|
Avec deux termes en 4k + 3
|
|
|
|
Une question de puissance?
|
|
|
|
|
|
|
Bilan
|
Un seul facteur en 4k + 3 ou en 4k + 3 à une puissance impaire suffit pour annuler toute possibilité
d'être un nombre somme de deux carrés. |
|
|
||
|
Un nombre est somme
de deux carrés si et seulement si chacun de ses facteurs premiers de la forme 4k + 3 a un exposant
pair. |
Si, lorsque pi = 4k +
3, Alors n est somme de 2
carrés. Autrement
dit: h(n) = 1. |
|
|
|
||
Voir Autre
formulation de ce théorème
Théorèmes
des deux carrés de Fermat
|
Tout nombre premier impair est la
somme de deux carrés si et seulement s'il est de la forme 4n + 1. La somme des carrés est alors
unique. Une condition nécessaire pour qu'un
nombre entier soit la somme de deux carrés est que tous ses facteurs premiers
soient de la forme 4n + 1. |
|
|
|||
|
Astuce
(a² + b²) (c² + d²) = (ad + bc)² + (ac - bd)² Exemple |
|||
|
|
2 x 32 x 5 x 72
= 4 410 |
= (2 x 7²) (3² x 5) = 98 x 45 = (7² + 7²) (3² + 6²) = (42 + 21)² + (21 – 42)² = 63² + 21² |
|
|
|
||
|
Si 2m est
la somme de deux carrés, alors m
l'est aussi. La preuve
découle du fait que x et y sont forcément de même parité. Leur somme et leur
différence sont divisibles par 2. |
Exemple 2m = 2² +
4² = 20 m = 1² +
3² = 10 |
|
|
|
|||
|
Si p est
premier (sauf 2), il existe k < p tel que:
a² + b² + 1² = k.p Vrai également si p est un nombre impair. Ce qui
veut dire que pour tout nombre premier, un de ses multiples est somme de
trois carrés, et a fortiori de quatre carrés. Ce qui
constitue un élément de preuve de la somme de quatre
carrés. |
Exemple pour 7 2 x 7 = 14 = 2² + 3² + 1 3 x 7 = 21 = 2² + 4² + 1 5 x 7 = 35 = 3² + 5² + 1 6 x 7 = 42 = 4² + 5² + 1 Exemple pour 11 1 x 11 = 11 = 1² + 3² + 1 3 x 11 = 33 = 4² + 4² + 1 6 x 11 = 66 = 1² + 8² + 1 = 4² + 8² + 1 9 x 11 = 99 = 7² + 7² + 1 10 x 111 = 110 = 3² + 10² + 1 |
||
|
Démonstration
de la propriété 1 Avec p =
2n + 1, formons les deux ensembles |
A { a² avec a de 0 à n} B {–b² – 1 avec b de 0 à n} |
||
|
Dans A,
il n'y a pas de couples congruent mod p |
|
||
|
Si
c'était le cas, on aurait les divisibilités suivantes: |
|
||
|
Or a – c
comme a + c sont inférieurs ou égaux à 2n et donc à p. |
|
||
|
Démonstration
de la propriété 2 |
|
||
|
Avec le
même procédé on démontre que: Dans B,
il n'y a pas de couples congruent mod p. |
|
||
|
Démonstration
de la propriété 3 Aucun
élément commun entre A et B |
Les éléments de A sont positifs alors que ceux de
B sont négatifs. |
||
|
La
réunion des deux ensembles compte 2n + 2 = p + 1 éléments. |
Il y a n + 1
éléments dans A, et n + 1 autres éléments dans B |
||
|
Chacun de
ces éléments, divisé pas p, donne au maximum p restes, or il y p + 1 valeurs |
Il y a forcément deux restes identiques (principe des
tiroirs) On dit: il existe deux éléments, un de A et un de
b qui sont congruents modulo p. |
||
|
Résultat
mis en forme: a² + b² + 1 divisible par p; autrement-dit, ce nombre est
multiple de p. |
|
||
|
La valeur
de k est inférieure à p. |
Sachant que a et b varient de 0 à n:
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/SomCaThe.htm |
![]()