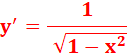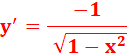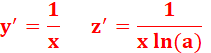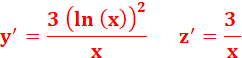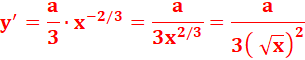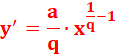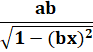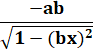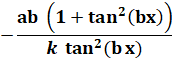Glossaire - dérivée

DÉRIVÉE

Approche

La voiture avance selon un profil de vitesse le long du parcours: en maths on remplace vitesse par dérivée.

La dérivée en un point d'une courbe exprime la tendance de la courbe en ce point: croissante, décroissante et, à quel rythme.

C'est un indicateur de la vitesse de variation de cette courbe.

Dérivée = valeur de la pente (ou coefficient directeur) de la tangente en un point d'une courbe.

Notion voisine

Notion duale

VITESSE, PENTE, TANGENTE, DÉRIVÉE

SURFACE (aire), INTÉGRALE

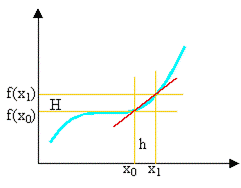
*Définition*	Une fonction f(x). Deux valeurs proches en x: x₀ et x₁ avec x₁ – x₀ = h La valeur de la fonction pour ces abscisses:
	f(x₀) et f(x₁) avec f(x₁) – f(x₀) = H La dérivée est: limite de H / h quand h tend vers 0
*Notations*	Dérivée de f(x) en a f'(a) ou df / dx La notation en y' (lire y prime) est de Newton	Dérivée de y = f(x) y' ou dy / dx Celle en d/d* est de Leibniz.*

Anglais

Derivative

For the real function f, if { f(a+h) – f(a) } / h has a limit as h 0, this limit is the derivative of f at a and is denoted by f ' (a)

The derivative is obtained as the limit of the Newton quotient

And this is equivalent to the notion of the gradient of a graph

The gradient of a graph = la pente de la courbe

From another point of view , the subject is concerned essentially with the rate of change of one quantity with respect to another

Dérivée des fonctions simples

Voir TABLE COMPLÈTE >>>

Polynôme

Fonction dérivée

y = a

y = a · x

y' = 0

y' = a

y = x

y = ax + b

y = ax² + bx + c

y' = 1

y' = a

y' = 2ax + b

Suite >>>

Inverse (x au dénominateur)

Fonction dérivée

Suite >>>

Trigonométrie (radians)	Fonction dérivée
y = sin x	y' = cos x
y = cos x	y' = - sin x
y = tan x
y = arcsin x
y = arccos x
y = arctan x

Suite >>>

Logarithmes	Fonction dérivée
y = ln x z = log_a (x)
y = (ln x)² z = ln(x²)
y = (ln x)³ z = ln(x³)
y = ln u

Suite >>>

Puissances – Exponentielle	Fonction dérivée
y = k^x	y' = k^x . ln (k)
y = e^x	y' = e^x
y = e^u	y' = u' · e^u
y = u^a	y' = u' · a · u^{a – 1}

Suite >>>

Racines

Fonction dérivée

Suite >>>

Voir Exemples de calcul de ces dérivées / Calcul de chemin /

Calcul de la racine cubique / Calcul par intégration

Table de primitives

Formule générale

*Fonction*	*Fonction dérivée*
y = uⁿ	y' = n . u^(n-1) . u'

Dérivée des fonctions composées

*Fonction*	*Dérivée*
y = u + v y = u .v y = u . v . w	y' = u' + v' y' = u.v' + u'.v y' = u'.v.w + u.v'.w + u.v.w'
y = 1 / v y = u / v	y' = - v' / v² y' = (u'.v - u.v') / v²
y = u	y' = u' / (2u)

y = g(u) & u = f(x)	y'_x = y'_u . u'_x On écrit aussi: dy/dx = dy/du . du/dx
y = ln u y = e^u	y' = u' / u y' = e^u . u'