|
|||||||||||||||||||||||||||||
![]()
À vraiment retenir
|
Les marées existeraient même si la Terre et la Lune n'étaient pas en mouvement. Le recours à la force centrifuge n'est pas nécessaire. L'équation de Newton sur la gravitation suffit. Motion does not raise tidal bulges
nor sustain them. Le mouvement ne crée pas les levées de marée ni
ne les entretient. D'après C. Johnson, Theoretical
Physicist, |
Citation
|
Les marées, ce
phénomène qu’un ancien appelait avec désespoir le tombeau de la curiosité
humaine, ont été rattachées par Laplace à une théorie analytique dans
laquelle les conditions physiques de la question figurent pour la première
fois – François Arago (1786-1853) |
Voir Pensées et Humour
|
Phénomène de MARÉE Explication de la double marée
quotidienne Semi-diurnal tide
Le calcul statique date de Newton, enrichi par Laplace pour le calcul dynamique. Le modèle1 s'est
grandement développé depuis, surtout en profitant de la puissance de calcul des ordinateurs.
Pourtant encore aujourd'hui, le phénomène de double marée est très rarement
bien expliqué. 1 Effets
à prendre en compte: gravité, forces centrifuges et de Coriolis dues à la
rotation de la Terre, le gradient de pression dans les océans, friction entre
l'eau et les fonds marins, forme des côtés, oscillations dues à la dynamique des océans (résonances), distance à la Lune,
inclinaison de l'orbite lunaire, etc. |
Merci à Pierre Vallet pour avoir attiré mon
attention sur les références (3) et (5)

|
|
||
|
Modèle statique |
Modèle dynamique |
|
|
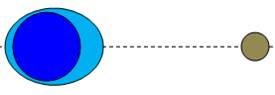
On suppose
la Terre et la Lune immobiles et on calcule les forces gravitationnelles
exercées par la Lune sur la Terre. On montre
que, par rapport à la force moyenne s'appliquant sur le centre de la Terre,
la force exercée de part et d'autres sont de même intensité mais opposées. Ce qui
explique correctement la double grande marée. Note: on
simplifie en mettant de côté l'effet du Soleil et toutes sortes d'autres
contributions. |
Les mouvements
de la Terre autour du Soleil ou sur elle-même sont sans effet sur les marées. En
revanche, la rotation du couple Terre-Lune autour
de son centre de gravité (centre de masse) est à prendre en compte car il est
susceptible de créer une force centrifuge
sur les points de la Terre Deux visions
|
|
|
Ce calcul à la Newton ne présente pas de
difficulté pour un élève de terminale |
Les calculs en dynamique sont d'un niveau supérieur.
Nous allons approcher intuitivement ces deux visions, l'une après
l'autre. |
|
Pour se lancer voyons quelques idées reçues
|
(1) La rotation de la Terre n'a aucun effet sur les
marées. (2) Le renflement des océans est dû à de petits mouvements
de grandes quantités de liquide, et non de grandes migrations. (3) L'effet de marée s'applique à tous les points du
globe terrestre. Il est plus manifeste sur les matériaux
"élastiques". (4) La marée haute n'est pas
obligatoirement en face de la Lune. (5) La seule attraction gravitationnelle suffit à
expliquer la double grande marée. (6) Les seules forces en action sont la gravitation
et la résistance à la traction interne aux matériaux. (7) La rotation du couple Terre-Lune crée une force
centrifuge qui est une force fictive associée au référentiel choisi. (8) La contribution à la marée de cette force
centrifuge est constante en intensité, en direction et sens. L'effet
gravitationnel n'est pas affecté. |
|
|
||
|
Idée |
Admettre
les forces centrifuges et constater qu'elles sont constantes. Explications inspirées de la référence (3) |
|
|
Lune Elle domine le Soleil |
La Lune
est plus petite, mais plus proche que le Soleil. Son effet gravitationnel,
agissant avec le carré de la
distance, est prépondérant. La Lune a
un effet d'attraction sur la Terre plus grand de son côté que du côté opposé.
|
|
|
Deux marées Première explication simple |
Ce n'est
pas ce que l'on observe ! Il y a une grande marée de chaque côté.
Autrement-dit: avec la rotation de la Terre, deux grandes marées par jour.
On pourrait dire de façon naïve que: par rapport
à une position d'équilibre des océans plaqués au sol uniformément par la gravité
de la Terre:
L'explication est un peu plus complexe. |
|
|
Rotation combinée du couple Terre-Lune
autour de leur centre de masse La clé du mystère : une rotation peu connue de la Terre, entrainée par
le mouvement de la Lune. |
La Lune
tourne autour de la Terre et l'inverse est vrai aussi. Le couple, comme tenu
par un axe rigide, tourne autour du centre
de gravité de l'ensemble. On dit aussi: centre de masse ou barycentre. Les
nuances entre ses notions sont sans importance pour notre propos. Analogies:
Imaginez la flèche d'une grue avec son énorme
contrepoids.
Imaginez un haltère dissymétrique qui tournerait
autour d'un pivot. La grande masse comme la petite décrivent des
cercles.
Évidemment, l'orbite de rotation de la Terre est
très petit comparé à celui de la Lune. Cette rotation particulière de la Terre induit
une trajectoire festonnée autour de son orbite
autour du Soleil. Notons que ce phénomène est vrai pour tout
couple, ou groupe, d'astres, y compris avec le Soleil. |
|
Centre de masse du couple Terre-Lune Il est interne au globe terrestre |
Du fait que
la Terre est 81 fois plus massive que la Lune, le centre de masse en rouge
est situé à un peu moins de 4 700 km (4 678 km) du centre de la Terre ou à 1
700 km sous
la surface.
La Terre tourne sur un cercle de rayon 4 700 km, La position du centre de masse varie en fonction
de la variation de la distance Terre-Lune. |
|
Force centrifuge Une bonne piste pour l'explication du double bourrelet |
Cette
rotation du couple Terre-Lune n'est pas sans effet sur la Terre et surtout
sur l'eau des océans. Elle crée une force centrifuge (flèches en rouge) qui
tend à éloigner les deux astres l'un de l'autre.
|
|
On récapitule: Deux types de forces On tient une bonne explication. On explique correctement le résultat,
mais … |
La force gravitationnelle
(en bleu) attire la Terre vers la Lune, plus intensément d'un côté que de
l'autre. La force
centrifuge (en rouge) est supposée égale de chaque côté.
La force résultante
(en vert) est identique de chaque côté. La
conjugaison des deux forces conduit à un effet de marée identique des deux
côtés. Pour satisfaire la condition de stabilité de
l'ensemble, la force gravitationnelle équilibre la force centrifuge au centre
de la Terre. |
|
Il y a un HIC ! … les forces centrifuges telles quelles ne peuvent pas expliquer le
phénomène Mais nous ne sommes pas loin. |
Si l'on
se souvient que le centre de masse du couple Terre-Lune est interne au globe terrestre,
alors: les forces centrifuges montrées en rouge sur la figure ne sont pas égales ni correctement orientées Situées
de part et d'autre du centre de masse, l'une d'elle doit être inversée
Ici, les forces centrifuges sont correctement
représentées, mais ce schéma ne peut pas expliquer la double marée. |
|
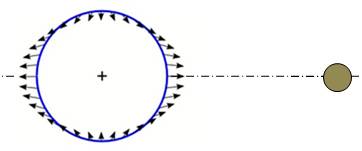
Forces centrifuges revisitées La contribution significative de la force centrifuge est constante |
Le couple
Terre-Lune est en rotation autour du centre de masse G. La force
centrifuge est représentée par le vecteur GM avec:
Le vecteur GO est constant quel que soit le point
M. Le vecteur OM est toujours de même intensité et
orienté vers un point de la circonférence, exactement comme le vecteur
gravité (dans l'autre sens). Son effet est de réduire uniformémént l'effet de
la gravité. Seul reste l'effet constant de OG sur tous les
points A. L'effet constant de la contribution de la force centrifuge
est donc confirmé. |
|
Confirmation Citation selon la référence (1) |
Thus, only the constant vector
GO contributes to the tidal force. Therefore, the given
explanation is correct. Ainsi,
seul le vecteur constant GO contribue à la force de marée. Par conséquent,
l'explication indiquée plus haut était bien correcte. |
|
|
||
|
Phénomène de résonance Étienne Ghys sur
son site décrit le phénomène dynamique qui change la représentation des
marées par rapport à la Lune. Statiquement vrai
Dynamiquement vrai Réalité entre les deux |
Point de vue de Newton: les figures qui montrent les renflements en face de la Lune sont
vraies en théorie statique. Point de vue de Laplace: ces figures sont fausses car l'océan qui enfle sous l'effet de l'attraction
lunaire, se relâche ensuite, créant de ce fait une oscillation d'une période
de 12 h et 25 minutes. Les
océans possèdent leur fréquence propre de l'ordre de 23 heures. Leur réponse
est plus lente que l'oscillation forcée par la Lune. En théorie,
les marées pourraient atteindre une opposition de phase par rapport à la Lune
(larges océans très profonds). Dans la
réalité, compte tenu de la taille et de la profondeur des océans, les
déphasages sont intermédiaires et complexes à déterminer. |
|
|
|
||
|
Idée |
Les
forces centrifuges sont fictives, sans
réalité physique, des pseudo-forces. Elles interviennent comme outils dans
les calculs avec référentiel non inertiel. Explications inspirées de la référence (5) |
|
|
Force fictive On devrait dire: effet centrifuge au lieu de force centrifuge. |
La force
centrifuge est celle que vous ressentez lorsque votre voiture prend un virage
vers la gauche et que votre corps est plaqué à droite. Elle se manifeste, par exemple, lorsque les
enfants s'amusent à faire valser des objets posés sur un plateau à fromage
rotatif. Cette
force est un artifice calculatoire utilisé pour rendre compte des phénomènes
dynamiques en rotation dans un référentiel
donné. En physique, on ne connait que les quatre forces fondamentales. En maths, on est habitué à admettre des entités
fictives comme intermédiaires de calcul. Cas des nombres complexes. L'auteur
de cette analyse (référence 5) introduit la force
centrifuge dans ses calculs et montre qu'elle ne change pas le résultat du
modèle statique. |
|
|
Référentiels et forces fictives Un accessoire de calcul utile dans les études de systèmes en rotation. |
Dans tout
référentiel fixe (ou inertiel ou
galiléen), la deuxième loi de Newton
s'applique: l'accélération d'un corps est égale au rapport entre la force qui
s'exerce sur lui et sa masse.
Dans un référentiel non inertiel, les lois du mouvement
de Newton ne sont vérifiées qu'en introduisant des forces fictives, les
forces d'inertie:
Aucune des trois lois de Newton ne s'applique et
surtout pas la troisième. Sans existence propre de l'action, il ne peut pas y
avoir une réaction. |
|
|
Couple Terre-Lune en référentiel fixe Les calculs montrent l'effet de double marée diurne sans recours aux
forces centrifuges |
Avec un
référentiel fixe (par rapport aux étoiles) centré sur le centre de masse, la
Terre tourne autour de ce point. En ignorant, la rotation de la Terre sur
elle-même, cette rotation de la Terre est en fait une translation. La Terre
présente toujours la même face à la Lune. Imaginez que vous observer le phénomène tous les
jours à la même heure. Rappelez-vous que la rotation propre de la Terre n'a
aucune influence sur la marée; seulement sur un renflement uniforme à
l'Équateur Rendez vous sur le site de la référence
(5) pour une animation. Vous y trouverez aussi les équations que je vous
épargne ici. Le
référentiel étant fixe, pas besoin de recourir aux forces fictives
centrifuges, et le résultat est le même qu'en calcul statique. |
|
Couple Terre-Lune en référentiel non inertiel Les calculs se compliquent mais donnent les mêmes conclusions. |
Avec un
référentiel au centre de masse, mais en rotation avec la Terre, la Terre
comme la Lune semblent stationnaires. Les
calculs font alors intervenir les deux forces d'inertie: la force centrifuge
et la force de Coriolis. Je vous renvoie à la référence (5) qui présente une
animation claire et tous les calculs (accessibles à des étudiants du
supérieur). Même avec
l'introduction des forces fictives et un calcul un peu plus compliqué, les
résultats sont toujours confirmés. |
|
Bilan |
Forces différentielles
de marée sur la planète Terre due à l'effet combiné des forces de gravitation
dues à la Terre et à la Lune. Avec le choix d'un référentiel inertiel, le
recours aux forces centrifuges est inutile.
La force différentielle doit être comprise comme
la différence entre la force au centre de la terre et celle au point
concerné. Notez que ces forces ont une composante radiale (compression) et
une composante tangente au cercle; c'est celle qui est susceptible de
déplacer les matériaux. Cette
même figure est tout aussi valable dans le cas du choix d'un référentiel non
inertiel en rotation. Les vecteurs sont alors la somme des forces
gravitationnelles et des forces centrifuges. C'est un choix légitime, mais
qui complique inutilement les choses. |
|
Conclusions Rien ne sera mieux que la traduction littérale du texte de Paolo
Sirtoli en référence (5) La condition de chute libre est celle que nous avons appelé situation statique,
ne faisant appel qu'aux lois de gravitation. |
À l'attraction de la Lune aux différents points de la surface de la
Terre, nous devons toujours soustraire un champ
uniforme, dont la valeur est égale à l'intensité de l'attraction de la
Lune au centre de la Terre. Pourquoi? La réponse réside dans le sens profond de la condition être en orbite autour d'un corps céleste.
Cette condition équivaut, dans tous les cas, à la condition de chute libre. La Terre est en chute libre vers la Lune, attirée par la force
gravitationnelle. C'est pourquoi la Lune ressent une accélération uniforme
dont l'intensité est (G.MLune / R²). Mais, puisque la Terre ne
tombe pas réellement le long d'une ligne droite mais est en orbite, cette accélération
linéaire se transforme en une accélération centripète (ω².c) d'intensité
uniforme. Le fait que la Terre tourne autour du Centre de masse ou sur
elle-même, jette malheureusement de la poussière à nos yeux. Ces effets ne
produisent aucune déformation de marée, ils ne font que nous embrouiller. |
|
La simple application des
lois de Newton relatives à la gravitation montre l'effet de double grande
marée. Les considérations sur la force centrifuge engendrées par le mouvement
Terre-Lune conduisent au même résultat. La version 1 donne une
explication intuitive en montrant les erreurs à ne pas commettre. La version 2 est
l'explication académique à adopter par tout expert scientifique. |
![]()
|
Retour |
|
|
|
Voir |
|
|
|
Sites généraux |
||
|
Sites calculs |
|
|
|
Cette page |
||
![]()