NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/01/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	MOTIFS & FORMES
Débutants Chiffre	NOMBRES UNIFORMES ou REPDIGITS			Glossaire Chiffre
INDEX MOTIFS Types de nombres Motif	Repdigits	Partitions	Carrés
		Sommaire de cette page >>> Partition en somme d'entiers consécutifs >>> Partition en somme de carrés >>> Somme de premiers consécutifs >>> Produits de repdigits tronqués premiers

NOMBRES UNIFORMES / REPDIGITS

Sommes / Partitions – Tables

Tables de partitions particulières de repdigits.

Bonus: produit de repdigits tronqués

Anglais: Rep-digit or Repdigit or Monodigit

Devinette

Quels sont les nombres repdigits à trois chiffres qui sont sommes des entiers de 1 à n ?

Solution

Partition en somme d'entiers consécutifs
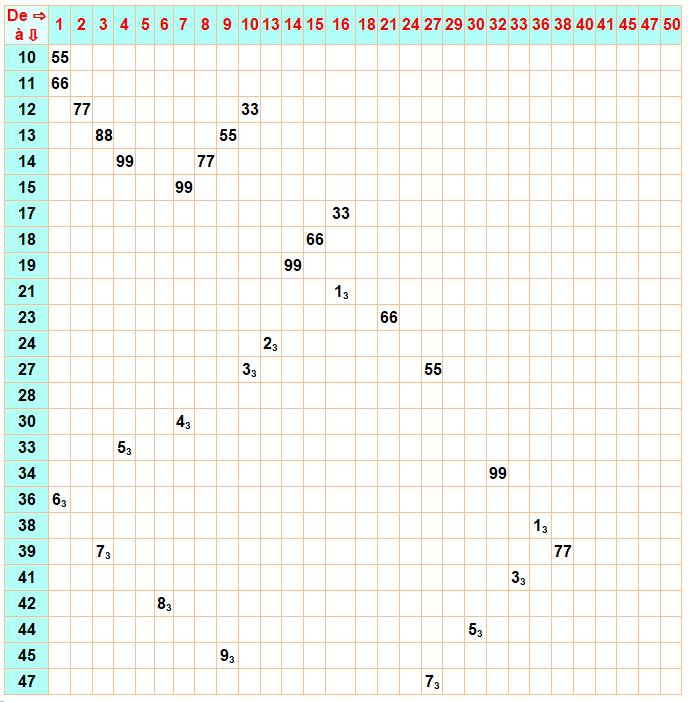
Nombres repdigits qui sont sommes d'entiers à partir de 1. Voir Formule de la somme des entiers	1 à 10 => 55 = 10 x 11 / 2 1 à 11 => 66 1 à 36 => 666 Aucun autre jusqu'à au moins 45 millions.
Nombres repdigits et somme d'entiers à partir de k Exemple de lecture: nombre 77 en (2, 12) => 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 77 Aucun autre jusqu'à un million. Rien commençant par les nombres manquants entre 1 et 50

Partition en somme / différence de carrés, de cubes
Somme de carrés Quelques repdigits sont sommes de carrés de nombres consécutifs. Ces configurations sont rares, sans doute les seules.	55 = 1² + 2² + 4² + 5² 77 = 4² + 5² + 6² 1 111 = 11² + 12² + 13² + 14² + 15² + 16² 44 444 = 71² + 72² + …+ 78² 444 444 = 51² + 52² + …+ 113²
Somme de cubes Encore plus rare pour les cubes	99 = 2^3 + 3^3 + 4^3 cf. 100 = 1^3 + 2^3 + 3^3 + 4^3
Différence de carrés Comme tous les nombres impairs, les repdigits impair sont la différence de deux carrés.	11 = 5 + 6 = 6² – 5² 77 = 38 + 39 = 39² – 38² 111 = 55 + 56 = 56² – 55²

Voir Carrés sommes de deux repdigits / Sommes de carrés consécutifs

Somme de premiers consécutifs
Seuls exemples jusqu'à un million et somme de six premiers.	222 8 888 777 777 88	= = = =	109 + 113 4 441 + 4 447 259 229 + 259 271 + 259 277 17 + 19 + 23 + 29

Voir Nombres premiers / Somme de premiers consécutifs

Produits de repdigits tronqués premiers
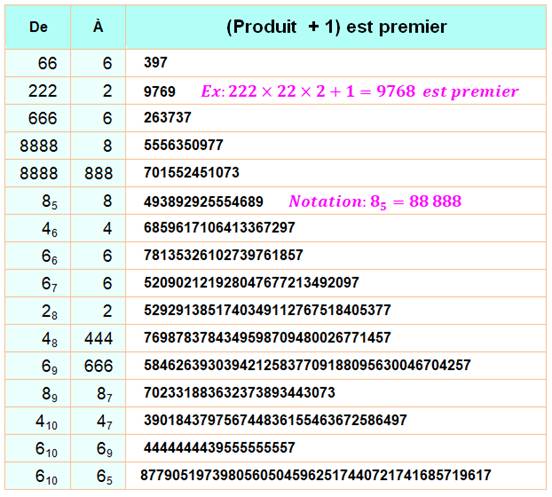
Un repdigit est multiplié par lui-même tronqué n fois. On ajoute 1. quels sont ceux qui sont premiers ? Le cas de 666 est particulièrement notable: Ces nombres sont premiers: 6 + 1 = 7 66 x 6 + 1 = 397 666 x 66 x 6 + 1

Devinette – Solution

Quels sont les nombres repdigits à trois chiffres qui sont sommes des entiers de 1 à n ?

La somme des entiers de 1 à n est repdigit à trois chiffres si:

Un test sur (222, 444, 666, 888) montre que seul 666 est la réponse. Alors k = 3 et n = 36, car 36 x 37 = 1332 et 1332 / 2 = 666.

Retour

Voir Somme des entiers / Somme des entiers consécutifs /

Divisibilité de la somme des entiers consécutifs

Retour	Repdigits
Suite	Repdigit en 6 (666) Repunits ou nombres uniformes Carrés des Repdigits Nombres magiques – Index
Sites	Repdigits – World Of Numbers – Patrick De Geest OEIS A010785 - Repdigit numbers, or numbers with repeated digits.
Cette page	http://villemin.gerard.free.fr/TABLES/aaaSomme/RepDigit.htm