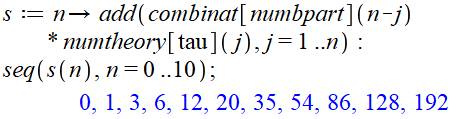Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 18/06/2023 M'écrire Brèves de Maths

INDEX Partition Calculs Dénombrement	PARTITIONS
	Approche	En bref et Index	S'y retrouver
	Quantité de partitions	Quantité de parts	Fonction génératrice

Faites un double-clic pour un retour en haut de page

Quantité de parts dans les partitions d'un nombre n Partitions du nombre 4: [1, 1, 1, 1], [1, 1, 2], [2, 2], [1, 3], [4] Nombre d'éléments (de termes, de sommants): 12.
	Sommaire de cette page >>> Quantité de parts >>> Liste des quantités de parts >>> Programme Maple	Débutants Nombres Glossaire Nombres

Quantité de parts

haut

Définition

Il s'agit de compter la quantité de nombres impliqués dans toutes les partitions d'un nombre.

Pour le nombre 5, par exemple, on compte 20 éléments (appelés sommants ou parts ou termes).

Propriété

Isolons le nombre le plus grand dans chacune des partitions (colonne ocre).

Ce sont les mêmes nombres que dans la colonne quantité (Q). La somme est évidemment la même.

Pour toutes les partitions d'un nombre

La quantité de parts est égale à la somme des sommants les plus grands.

Les sept partitions du nombre 5

1, 1, 1, 1, 1	5
1, 1, 1, 2	4
1, 2, 2	3
1, 1, 3	3
2, 3	2
1, 4	2
5	1
Total	20

Mise en évidence des grands sommants

Partitions		Q
1, 1, 1, 1	1	5
1, 1, 1	2	4
1, 2	2	3
1, 1	3	3
2	3	2
1	4	2
	5	1
Total	20	20

Liste des quantités de parts		haut
Pour n de 0 à 57	0, 1, 3, 6, 12, 20, 35, 54, 86, 128, 192, 275, 399, 556, 780, 1068, 1463, 1965, 2644, 3498, 4630, 6052, 7899, 10206, 13174, 16851, 21522, 27294, 34545, 43453, 54563, 68135, 84927, 105366, 130462, 160876, 198014, 242812, 297201, 362587, 441546, 536104, 649791, 785437, 947812, 1140945, 1371173, 1644136, 1968379, 2351597, 2805218, 3339869, 3970648, 4712040, 5584141, 6606438, 7805507, 9207637, … Voir OEIS A006128

Programme Maple			haut
	But Principe de calcul du nombre de parts. Commentaires Exemple avec 5. Le nombre de parts sera en s. Exploration des partitions des nombres de n–1 à 0 en a. Quantité de partitions des nombres de 1 à j en b. Le produit en c et le cumul en s. Demande d'impression. Résultat La quantité de parts est progressivement formée en colonne de droite de la liste pour aboutir à 20.
		Génération de la liste Fonction de calcul de s sur le principe exposé ci-dessus. Demande de calcul d'une suite (seq).

Voir Programmation – Index

Haut de page (ou double-clic)

Retour	Addition Addition – Glossaire
Voir	Partitions – En bref et orientation Partitions – Index Autres partitions particulières (Goldbach, Zeckendorf) Partitions distinctes et théorème des nombres pentagonaux
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/PartPart.htm