|
|||||||||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ
p Curiosités et magie ! |
Voir Règles
générales
|
|
|
|
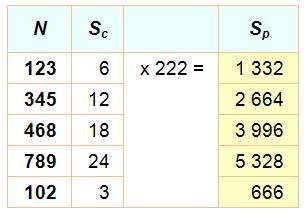
Théorème Avec un nombre de trois chiffres distincts, la somme S
des permutations divisée par la somme s de ses chiffres est une
constante égale à 222. Exemple
|
|
|
|
|
|
|
|
|
|
|
|
Nombre quelconque de
trois chiffres distincts
Nombre à chiffres
répétés
Exemple 112 => 112, 121, 211 => Somme:
444 222 => 222 => Somme:
222 |
|
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Cette page |
![]()