NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/05/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	DIVISION
Débutants Division	Divisibilité			Glossaire Division
INDEX Divisibilité	Introduction	Critères généraux	Polynômes	Fermat
	Puissance	Forme n^k + k^n	Forme n^x ± y	Wilson
	Somme	x (x + a) (x+ b)	Formes diverses
		Sommaire de cette page >>> Divisibilités par nombres croissants >>> À noter: carrés, factorielles, répétitions >>> Divisibilités par formes croissantes >>> Divisibilité par 73 et 137 – démo >>> Divisibilité par 91 >>> Formes littérales >>> En puissance de 2, 3 et 5 >>> Nombres consécutifs >>> Carrés et factorielles

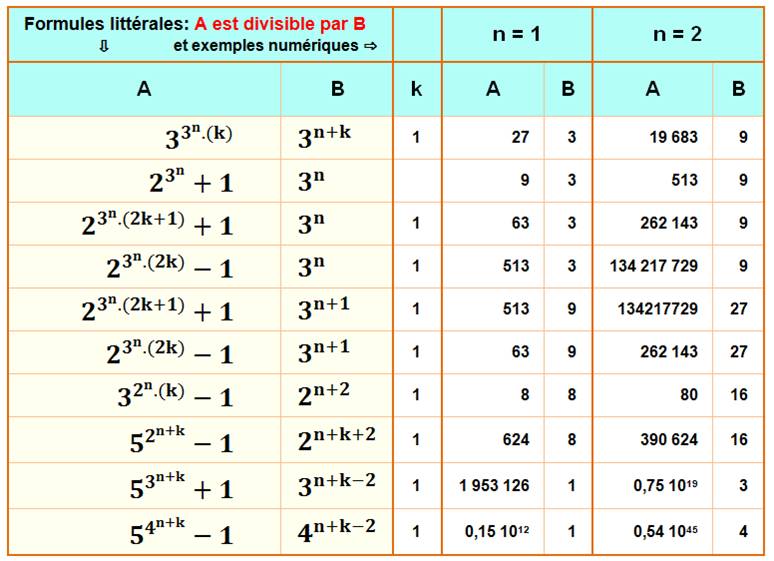
DIVISIBILITÉ

des EXPRESSIONS ALGÉBRIQUES

par un nombre donné

Trouver des formes algébriques divisibles par un nombre en utilisant les théorèmes de Fermat et de Wilson ou en utilisant la méthode par de déduction par induction.

Rappels: la barre verticale veut dire: divise; le chapeau ^ signifie puissance: 2^{2^3} = .

DIVISIBILITÉS PAR NOMBRES CROISSANTS

Divisible par	Formes divisibles	Avec / Condition / Commentaires	Démo
2	n^2 – n = (n – 1) n n^2 + n = n (n + 1) n^k – n = (n – 1) n . K	Produit de deux nombres consécutifs. Alors, l'un d'eux est forcément pair. Il existe de nombreuses formes paires Voir Nombres triangulaires / Nombre et leurs puissances	démo
	F3k	Les nombres de Fibonacci de rang 3k sont pairs.	Autres
3	1^n + 2^n	Pour n impair.	démo
	2^n – 1	Divisible par 3 pour n pair Divisible par 5 pour n = 4k Divisible par 7 pour n = 3k Divisible par 63 pour n = 6k Divisible par 11 pour n =10k	démo
	4^n – 1 = 2^2k – 1		démo
	n (2n² + 7)		démo
	n^3 + 2n
	5^n – 2^n		démo
	a b ( a² – b² )		démo
	2^2^n + 5		démo
	381, 381111, …		démo
	Fermat + 10		démo
3^n	3^n 33…3n	Divisibilité d'un repdigit de n chiffres.	démo
4	(2k + 1 ) + (2k + 3)	Somme de deux impairs consécutifs.
	(2k)²	Carré d'un nombre pair.	démo
	a² + 3 et a² – 1	(+3) pour a pair et (-1) pour a impair	démo
	5^n – 1
	x^2 – y^2 = (x – y) (x + y)	Si (x – y) pair. Car, alors, x et y sont de même parité et leur somme est aussi paire.	démo
	(n + k)² – (n – k)² = 4 k n (a.n + k)² – (a.n – k)² = 4 k.a.n		démo
	a = ...cdu	avec 2d + u multiple de 4.
	7^n – 3^n	= (7 – 3) (…) = 4 (…)	démo
	6 x 7^n – 2 x 3^n	Vraie pour les coefficients 2, 6, 10, …
	ne divise pas n² + 1 ne divise pas n² + 2	Si n est pair 4 divise n². Si n est impair 4 divise n² + 3.
5	3^3n+1 + 2^n+1		démo
	1^n + 2^n + 3^n + 4^n	Pour n impair.	démo
	2^2n+1 + 3^2n+1
	3^n – 2^n	Pour n pair.	démo
	7^n – 2^n	Tout nombre en a^n – b^n est divisible par a – b.	démo
	8^n – 3^n
	11^n – 6		démo

6	(n – 1) n (n + 1) = n^3 – n n (n^2 + 5) = n^3 + 5n	Un produit de trois nombres consécutifs est divisible par 3! = 6. La relation demeure en ajoutant 6k. Par exemple -1 + 6 = 5. Voir Nombres tétraédriques	démo démo
	n^3 – n = (n – 1) n (n + 1) n^2k+1 – n = (n – 1) n (n + 1) K	Voir Nombre et leurs puissances	démo
	n (n + 1) (n + 5) n (n + 4) (n + 5) n (n + 1) (n + 2) (n + 4) etc.	Démo en examinant n = 6q + r pour les six valeurs du reste r.	démo
	n (n + 1) (2n + 1) = 2n^3 + 3n^2 +n	Expression utilisées pour la somme des carrés des entiers	démo
	(n + 2k)² – (n – 2k)² = 8 k n		démo
	5n^3 + n
	(n + 1)^3 – n^3 – 1	Différence entre cubes successifs	démo
	7^n – 1	Tout nombre en a^n – b^n est divisible par a – b.	démo
7	n^7 – n = n (n^6 – 1)
	n^6 – 1 n^6k – 1	Divisible par 7 sauf pour n = 7k (Fermat). Divisible par 9 sauf pour n = 3k. Divisible par 4 pour n impair
	1^n + 2^n + 3^n + 4^n + 5^n + 6^n	Pour n impair.	démo
	2^3k – 1		démo
	4^n – 3^n	Pour n pair. Voir 35 et 77	démo
	3^2n – 2^n
	3^2n+1 + 2^n+2		démo
	6^n – 1 = 2^3k – 1
	a, b, a + b ou a – b	Dans un triplet de Pythagore	>>>
		= 1001 x 7 x 11 x 13 x	>>>
8	x (x + 1) (x + 3) (x + 6) x (x + 2) (x + 3) (x + 5) x (x + 3) (x + 5) (x + 6)		>>>
	n² – 1 = (n – 1) (n + 1)	Si n impair. Car, alors, produit de deux pairs successifs dont l'un est divisible par 4.	démo
	4^n – 2^n = 2^n (2^n – 1) 4^n + 2^n = 2^n (2^n + 1)	Pour n < 2 Divisible par 48 pour n pair ou impair >>>
	3^n – 1	Pour n pair. Note: 3^n – 1 est, lui, toujours pair, car étant factorisable en (3 – 1) k.	démo
	3^2n – 1
	3^2n + 7 5^2n + 7 (2k+1)^2n + 7		démo
	3^n + 7^n – 2
2^n+2	3^2^n – 1	Exemple pour n = 1 => 8 | 8.	démo
9	(n–1)^3 + n^3 + (n+1)^3	Somme de trois cubes successifs. Divisible par 18 pour n = 2k	démo
	a^3 + 1 et a^3 – 1	(+1) pour a = 2 mod1 et (-1) pour a = 1 mod 3	démo
	1^n + 2^n + 3^n + 4^n + 5^n + 6^n + 7^n + 8^n	Pour n impair. Propriété générale pour tous les nombres impairs.	démo
	5^n – 4^n	Pour n pair. Divisible par 11 pour n = 5k.	démo
	5^n + 4^n	Pour n impair. Divisible par 63 pour n = 3 + 6k.
	10^n + 3 . 4^n+2 + 5	Si 4 divisible par 4 pour n>1; Si 2 divisible par 6 et par 60 pour n = 2k>2; Si 0 divisible par 8 pour n>2 et par 56 pour n = 2k>2.
	N – rN	Nombre N et son retourné rN. N = 10a + b et rN = 10b + a dont la différence est 9a – 9b.	démo

11	aa…abb…b	Avec quantité paire de chiffres	>>>
	n^4 + 3n^2 – 7	Divisible par 11 pour n = {4, 5, 6, 7} + 11k Divisible par 3 pour n = {1, 2} + 3k Divisible par 7 pour n = {0, 2, 5} + 7k Divisible par 9 pour n = {4, 5} + 9k
	n + r	Un nombre ajouté à son retourné est divisible par 11 si sa quantité de chiffres est paire.	démo
	6^n – 5^n	Divisible par 11 pour n pair Divisible par 7 pour n = 3k Divisible par 77 pour n = 6k	démo
	6^n + 5^n	Divisible par 11 pour n impair
	3^n+0 – 4^4n+0	Si 0 et 0 + 5k divisible par 11 Si 1 et 4 + 5k divisible par 11 Si 2 et 3 + 5k divisible par 11 Si 3 et 2 + 5k divisible par 11 … Divisible par 77 pour {0, 0}P, {1, 4}I, {2, 8}P, {3, 12}I, {4, 1}P… L'indice impose que n soit pair ou impair.	démo
	10^2n – 1 + 1	Ces nombres en 10…01, comportant une quantité paire de 0, sont divisibles par 11. Divisibles aussi par 91 pour n = 2 + 3k.
12	(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)	Produit des différences de quatre nombres distincts.	démo
	(3n + a)² – (3n – a)²	Le développent donne 12 a.n.
	(n+1)^3 + n^3 – (n–1)^3 – (n–2)^3 – 10	Avec cubes de quatre nombres successifs.	démo
	x (x + 1) (x + 2) (x + 5) x (x + 1) (x + 4) (x + 5) x (x + 1) (x + 5) (x + 6) x (x + 3) (x + 4) (x + 5) x (x + 3) (x + 5) (x + 5)		>>>
	p + p'	Somme de deux nombres premiers jumeaux.	démo
13	7^n – 6^n	Pour n pair.	démo
	31^n + 1 + 18^n – 1 31^i x n + 1 + 18^i x n – 1	Vraie pour (i, i + 4k)
	p^12 – q^12	Pour p et q non divisibles par 13.
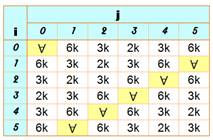
14	3^4n + 2 + 5^2n + 1 3 ^i x n + 2 + 5 ^j x n + 1	Vraie pour i + j = 6k (jaune dans le tableau). Vraie pour toutes les valeurs i et j du tableau avec n = {quelconque, 2k, 3k, 6k}.
15	(n+1) (n+3) (n+5) (n+7) (n+9)	Avec n pair (5 nombres impairs consécutifs).	démo
	4^n – 1	Divisible par 15 pour n pair; Divisible par 11 pour n = 5k; Divisible par 4095 pour n = 6k; Divisible par 165 pour n = 10k.	démo
	8^n – 7^n	Pour n pair	démo
	3n^5 + 5n^3 + 7n	Divisible aussi par 30 pour n pair.. Voir Entier curieux	démo
	2^(4n) – 1	Divisible aussi par 1365 = 7 x 13 x 17 pour n =3k.
16	n^4 + 4^n	Pour n pair.	démo

24	p² – 1	p premier n >3 ou mieux p impair non multiple de 3 Voir Cas de n² + 1	démo
	n^3 – n = (n–1) n (n+1)	n impair et n premier. Divisible par 6 = 3! pour tout n.	démo démo démo
	n (n+1) (n+2) (n+3)	Quatre nombres consécutifs. Un produit de quatre nombres consécutifs est divisible par 4! = 24
	n (n^2– 1) (3n + 2)	Divisible aussi par 48 pour n = {7, 8, 9, 10} + 8k
	n (n^2– 1) (i . n + j)	Pour (1,2), (1,6), (2,0), (2,4), (3,2) … Divisible par 48 pour (2,4); Divisible par 36 pour (3,0); Divisible par le double sous condition comme: tous sauf pour 2 + 4k.
	5^n – 1	Pour n pair Divisible par 15 624 = 7 x 8 x 9 x 31 pour n = 6k	démo
	n^x– n ^x – 2	x > 4 Vraie pour x = 3 ou 4 et n 2 + 4k
	n^14 – 1	n premier n >3
	p^2 – 1	p premiers p > 3	>>>
	p^2 – q^2	p & q premiers p & q > 6	>>>
	3^n + 7^n – 10	Si – 2 divisible par 8; Si – 4 divisible par 6; Si – 6 divisible par 4; Si – 7 divisible par 3; Si – 8 divisible par 2.
	2 . 7^n + 3 . 5^n – 5	Divisible aussi par 24 pour (1,5) et (3,2) avec n pair.	démo variante
25	7^2n + (2^3n-3) (3^n-1)
27	10^n+1 – 9n – 10 3 + 33 + … + 33…3n	33…3n est composé de n fois le chiffre 3 Voir Repdigit	démo
29	Fn + Fn+1 + … + Fn+13	Somme de 14 nombre de Fibonacci consécutifs	>>>

30	n^5 – n	Divisible aussi par 60 pour n pair.	démo
31	2^5n – 1		démo
32	3^2n + 24n – 1	Et divisible par 64 pour n pair.
33	33 . xyzt	Permutation circulaire	Nb33
35	6^n – 1	Pour n pair. Divisible par 5 pour tout n et par 7 pour n pair.	démo
	4^n – 3^n	Pour n = 4k. Divisible par 7 pour n pair. Jamais divisible par 2 ou par 3.	démo
	3^6n – 2^6n		démo
37		Car = 111 x a = 3 x 37 x a
	37 . xyz	Permutation circulaire	Nb37
41	41 . xyztu	Permutation circulaire	Nb41
42	n^7 – n	Divisible aussi par 84 sauf pour n = 2 + 4k.	démo
43	6^n+2 + 7^2n+1
48	7^n – 1	Pour n pair Divisible aussi par 96 pour n = 4k.	démo
	4^n – 2^n = 2^n (2^n – 1) 4^n + 2^n = 2^n (2^n + 1)	Divisible par 48 pour n pair > 3 et par 768 = 2^8 x 3 pour n pair >7. Normal avec le facteur 2^n. Divisible par 48 pour n impair > 4 et par 768 pour n impair >8.
	n (n^2+ 20) = n^3 + 20n	Pour n pair. Divisible par 96 pour n = 8k.
49	2^3n+3 – 7n – 8	Divisible aussi par 96 pour n = 2k.
60	a.b.c	Si a, b et c forment un triplet de Pythagore
63	2^n – 1	Divisible par 63 pour n = 6k. Divisible par 3 pour n pair.
	8^n – 1 = 2^3n – 1	Pour n pair. Divisible par 7 pour tout n.	démo
66	n^11 – n		démo
73		Car 73 divise 10001.	démo
75	10^n – 5^n = 5^n (2^n – 1)	Pour n pair >1 Divisible par 25 pour tout n.	démo
77	4^n – 3^n	Pour n = 10k. Divisible par 7 pour n pair.	démo
80	9^n – 1	Pour n pair. Divisible par 8 pour tout n. Divisible par 160 pour n = 4k.	démo
81	10^n+1 – 10 – 9n	Divisible aussi par 162 pour n = 2k.
84	n^7 – n = n (n^6 – 1)	Divisible par 84 sauf pour n= 2 + 4k. Divisible par 42 pour tout n.
91	p^12 – q^12	p (>1) et q non divisibles par 91. p = 2 et q = 1 2^12 – 1 = 2095 = 91 x 45	>>>
		1001 = 11 x 91	>>>
99	10^n – 1 = 999…9	Divisible par 9 pour tout n. Divisible par 99 pour n pair.	démo
	100^n – 1 = 9999…99	Divisible par 99 pour tout n.
	r – n	Un nombre soustrait de son retourné est divisible par 99 si la quantité de chiffres est impaire.	démo

111		Les nombres ayant leurs chiffres égaux par paquets de trois sont divisibles par 111.	>>>
120	(n–2) (n–1) n (n+1) (n+2)	Cinq nombres consécutifs. Un produit de cinq nombres consécutifs est divisible par 5! = 120	démo
	(n–1) n (n+1) (n+2)	Sauf pour n = 4 + 5k	>>>
	11^n – 1	Pour n pair. Divisible par 10 pour tout n.	démo
	n^5 – 5n^3 + 4n = (n – 2)(n – 1) n (n + 1)(n + 2)	Pour n > 2 Divisible aussi par 840 sauf pour {10 ou 11} + 7k.	démo
127	2^7n – 1		démo
133	11^n+2 + 12^2n+1	133 = 7 x 19.	démo
137		10001 = 73 x 137	démo
138	n^23 – n		démo
143	12^n – 1	Divisible par 11 pour tout n. Divisible par 13 pour n pair. Divisible par 143 pour n pair.	démo
168	13^n – 1	Pour n pair. Divisible par 12 pour tout n.	démo

222	Sp / sc	Somme des permutations sur somme des chiffres.	démo
240	n^4 – 1	n premier n > 5	démo
	n^5 – n	Divisible par 240 pour n impair. Divisible par 30 pour tout n. Divisible par 8 pour n impair.	démo
	(n–2) (n–1) n (n+1) (n+2)	n pair	démo
	n^8– n ^4 n^a– n ^a – 4	Divisible par 240 pour tout n. D'une manière générale pour a > 7.
264	n^10 – 1	n premier > 3 et 11.	démo
282	n^47 – n
480	n^8 – 1	n premier > 5
	n^9 – n = n ( n^8 – 1)	n impair
504	(c – 1) c (c + 1)	c est un cube = n^3	démo
	p^6 – 1 = (p^3 – 1)(p^3+ 1)	n premier >3, sauf 7	démo
	n^7 – n = n (n^6 – 1)	n premier > 3
	n^a– n ^a – 4	Pour a > 8
510	n^17 – n		démo
512	3^2n+5 + 160n² – 56n – 243	Pour tout n. Divisible par 2048 pour n impair.	démo
576	5^(2n + 2) – 24n – 25	Pour tout n. Divisible par 1152 pour n = {3 ou 4} + 4k	démo
641	F5 = 2^2^5 + 1	Fermat #5	démo
720	n^2 (n^2– 16)	Vraie pour n = 4, 6, 14, 24, 30, 36, 40, 50 …
798	n^19 – n		démo
840	n^7 – 7n^5 + 14n^3 – 8n	Divisible aussi par 1680 sauf pour n = {3 ou 5 } + 8k.
870	n^29 – n

1 590	n^53 – n		démo
1 806	n^43 – n		démo
2 304	7^2n – 48n – 1	Note: 2304 = 48² Divisible aussi par 4608 pour n = {1 ou 4 } + 4k.
2 730	n^13 – n	Note: 2730 = 2 x 3 x 5 x 7 x 13 Divisible aussi par 5460 sauf pour n = 2 + 4k.	démo
2 880			démo
13 530	n^41 – n		démo
14 322	n^31 – n		démo
33 744	n^36 – 1	Si n premier avec 2, 3, 19 et 37 Note: 33 744 = 2^4 x 3 x 19 x 37
65 520	n^12 – 1	n premier > 10
1 919 190	n^37 – 1

Voir Autres formes polynômiales en équations diophantiennes

Formes littérales

	a^2 b^2	si a b	>>>
p	n^p – n	p premier
p	n^p-1 – 1	p premier n premier avec p Fermat	démo
p	(n + m)^p – (n^p + m^p)	p premier	démo
p	n^p + m^p	p premier et p divise n + m	démo
p	(p – 1)! + 1	p premier Wilson
r !	n(n+1)(n+2) …(n+r)	Produit de r nombres consécutifs	démo
n²	(n + 1)^n – 1
(n – 1)²	n^k – 1	si k est divisible par n – 1 et n >1
p² + p + 1	p^n+1 + (p+1)^2n-1
2^b – 1	ne divise jamais 2^a – 1	a et b > 2
a^2^n + 1	a^2^m – 1	m > n

D'autres formes

N	1^n + 2^n + 3^n + ... + (N–1)^n	Pour tout N impair et n impair	>>>
(a – b)	a^n – b^n	Pour tout n	>>>
(a – b) (a + b)	a^n – b^n	Pour n pair	>>>
a² + b²	(a^4n – b^4n)

En puissance de 2, 3 et 5
A est divisible par B pour tout n et k entiers positifs.

Nombres consécutifs
La somme de k nombres consécutifs est divisible par k si k est impair et par k/2, si k est pair. Le produit de k nombres consécutifs est divisible par factorielle k. >>>	S = n + n+1 + n+2 + … + n+k S = kn + (1 + 2 + 3 +…+ k) S = kn + k (k + 1) / 2 S = k { n + (k + 1) / 2} Divisible par k si k+1 est pair; soit k impair.

Carrés, factorielles
Différence de deux carrés N, la différence des carrés de a et b, est divisible par la somme et par la différence de a et b.	N = a² – b² = s . e s = a + b e = a – b
Factorielles Produit de factorielles.	Soit a = (p!)^q. q! et b = (q!)^p. p! Alors n = (p . q)! est divisible par a et b.

Suite	Formes diverses Critères généraux Divisibilité – Index Somme de q nombres divisible par q Autres formes polynômiales et équations diophantiennes
Voir	Calcul mental – Index Carrés – forme générique Divisibilité dans une suite de nombres Divisibilité des formes n^x - 1 Divisibilité par n = 24, 42 … Fermat Formes polynomiales Géométrie – Index Multiplication Nombres à motifs Nombres abondants  Nombres magiques Nombres parfaits  Nombres répétés Puissances de 2 Puissances – format Rep-unit Théorie des nombres – Index Triplets de Pythagore – Divisibilité
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/DivisiFo.htm