|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Les quatre opérations – Débutant
Multiplications et divisions
par 10, 100 …
![]()
|
DIVISION - INITIATION Comment bien démarrer avec les divisions Toutes les étapes et pièges, pas à pas.
|
Voir
Les quatre opérations – Junior / Évaluation de CM1
|
Réponse: 3 ou 0. En
effet => Sur le même modèle fallacieux, on
pourrait prétendre que le double de 3
est 8 et, que celui de 0 est 8! En anglais Teacher
asks student: What is the half of 8 ? Student: Miss horizontally or vertically ? Teacher: What do you mean ? Student: Horizontally it is 0 and vertically it
is 3. |
Voir
Pensées & humour
|
Comprendre
la division sans même savoir compter |
|
|
|
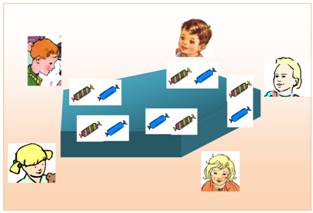
Clément,
le plus jeune frère ne sait pas compter. Mais, il sait déjà défendre ses
intérêts.
Chacun
doit avoir la même part, dit Clément. Cléo,
le plus grand frère, prétend avoir une bonne méthode pour y arriver.
Clément
est content, il visualise et comprend que chacun à un bonbon. Oui,
mais Cléo en a encore dans la main.
Cléo
distribue un nouveau bonbon à chacun. Il
fait le tour. Et,
arrivé à lui-même, se donne un bonbon qui se trouve être le dernier a
distribuer.
Il ne
voit rien à redire. Il
est content et comprend que chacun a deux bonbons et qu'il n'en reste pas.
Cléo, qui va déjà à l'école primaire, sait qu'il a
réalisé un partage, une division. |
10 partagé
en 5 donne 2 chacun et il
ne reste rien. Ou en écriture abrégée 10 / 2 = 5 Vérification 5 x 2 = 10 |
|
|
Mais,
il n'y pas assez de bonbons pour faire tout le tour. il ne peut pas en donner
3 à chacun.
Les
deux plus petits? Toujours les mêmes qui sont chouchoutés! Ou
les deux plus grands? Ils ont plus de besoins! Et,
moi, s'écrie Louise, la troisième, on m'oublie … |
12 divisé
par 5 donne 2 chacun et il ne reste 2. Ou en écriture abrégée
12 / 2 = 5 reste 2 Vérification 5 x 2 + 2 = 10 + 2 = 12 |
|
Comment
poser la division |
|
|||||||
|
|
|
|||||||
|
|
|
|||||||
|
Il
vient de distribuer 5 bonbons. Il
lui en reste 10 – 5 = 5 bonbons. |
|
|||||||
|
Ce
n'est pas un tour, mais deux tours qu'il peut effectuer. D'ailleurs,
après cette deuxième tournée, il ne lui reste plus rien 10 – 2x 5 = 0. |
|
|||||||
|
||||||||||||||||||||||||||
|
27 / 13 = 2 reste 1 ou 27 = 13 x 2 + 1 |
|
Avec
un reste ce n'est pas plus difficile |
|
|||||||
|
Nous sommes 5. |
|
|||||||
|
|
|
|||||||
|
|
|
|||||||
|
Primaire (calcul) Écritures
équivalentes de la division:
Le saviez-vous ? Le "deux-points" a été introduit en 1684 par Leibniz et il est en usage en Europe sauf
dans les pays anglo-saxons qui utilisent l'obélus (fraction avec deux
points). Il est recommandé d'utiliser l'écriture fractionnaire sous sa forme
classique ou linéaire. Vinculum:
symbole
de la fraction Obélus: symbole de la
division* * Ce symbole est
banni par la norme internationale ISO 8000-2
(2-9.6). Il est toujours présent sur les calculatrices Attention: une barre verticale veut dire divisible en arithmétique et tel
que en algèbre Les anglo-saxons notent: Résumé
Les
mathématiciens, les scientifiques, les ingénieurs … privilégient la barre de
fraction (écriture professionnelle) ou la barre oblique (écriture linéaire), conformément
à la norme ISO.
Secondaire (arithmétique et algèbre) La
division sans reste est dite division exacte. On
note: 5/2 = 2,5 (décimales
en nombre limité) ou 5/3 = 1,666… ou La
division avec reste est appelée division
euclidienne. On
note: 7 = 2 x 3
+ 1 ou 7:3 = 2 r
1 = 2 R 1 (r
pour reste ou remainder en anglais) ou 7/3 = 2 +
1/3 En algèbre, la division se note:
En programmation, la division entière
est notée: En python: 7//3 retourne 2, le quotient. Certains langages (Wolfram) notent le quotient: 7\3 =
2. En Maple:
iquo(7,3) retourne 2 et irem(7,3) retourne 1, le reste. En arithmétique, le reste de la
division est noté:
|
Voir Division euclidienne / Modulo / DicoMot / Notations de la
multiplication
|
Quand
le résultat a plusieurs chiffres |
|
|||||||||||||||||||||||||||||||
|
Nous sommes 5. Combien chacun? |
|
|||||||||||||||||||||||||||||||
|
Une
règle bien pratique qui nous demande de balayer les chiffres du nombre à
diviser de gauche à droite.
Je
vérifie que ma division se présente bien. Le reste (2) doit être inférieur au
diviseur (5). Car autrement, j'aurais pu faire au moins une distribution
supplémentaire. |
|
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
Le
reste étant nul, nous avons tout distribué. La division est terminée. |
Et voici le travail: 120 / 5 = 24 Vérification: 24 x 5 = 120 |
|||||||||||||||||||||||||||||||
|
Quand le résultat a
plusieurs chiffres et
avec reste |
|
|||||||||||||||||||||||||
|
Nous sommes 5. Combien chacun?
Le
reste final (2) est inférieur au diviseur (5). Il
est impossible de procéder à une nouvelle distribution à chacun. La
division est terminée. |
Résultat: 122 / 5 = 24, reste 2 Vérification: 24 x 5 + 2 = 122 |
|||||||||||||||||||||||||
|
Autre exemple
Nous sommes 5 Combien chacun?
ou
par le fait que le nombre à diviser est inférieur au diviseur. Il
suffit d'abaisser un chiffre en plus s'il en existe encore. Sinon
la division est terminée. |
Résultat: 12004 / 5 = 2400, reste 4 Vérification: 2400 x 5
+ 4 = 12004 |
|||||||||||||||||||||||||
|
Il
n'y a pas assez pour soustraire! Que faire? |
|
|||||||||||||||||||||||||||||||
|
Nous sommes 5. Combien chacun? Illustration
d'un nombre à diviser inférieur au diviseur. |
Résultat: 12014 / 5
= 2402, reste 4 Vérification: 2402 x 5
+ 4 = 12014 |
|||||||||||||||||||||||||||||||
|
Notation à la
française
|
|
|||||||||||||||||||||||||||||||
Voir la
division de 654 par 5 en détail (euclidienne et décimale)
Bilan
|
Nous
savons effectuer des divisions d'une manière générale. Quelques cas
particuliers nous attendent encore sur les pages
suivantes, mais les principes de base sont ceux indiqués ici. Pour
nous rassurer, nous pouvons vérifier la vraisemblance de nos résultats en
utilisant la preuve par neuf. Avec
l'usage des calculettes, la pratique de la division se perd. Raison de plus
pour y porter une attention particulière. C'est aussi un bon entraînement au calcul mental. |
Orientation

Histoire archi-célèbre
du reste du papier peint
|
Il
veut refaire la tapisserie et s'adresse à son voisin qui dispose du même
appartement et qui vient de changer le papier peint il y a moins de trois
mois. -
Combien de rouleaux de dix mètres avez-vous pris ? -
Vingt-huit. Il
achète les vingt-huit rouleaux, s'active à
poser le papier et à la fin, il lui reste encore pas mal de rouleaux. -
Je suis surpris, dit-il au voisin. J’ai tapissé toute la pièce, et il me
reste six rouleaux… -
Ben, moi aussi, j'ai eu la même chose! |
![]()
|
Voir suite en |
|
|
Voir résumé en |
|
|
Très utile |
|
|
Voir |
|
|
Cette page |