|
|||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES de FERMAT Diviseurs
Les
diviseurs sont également des puissances de 2 plus 1. |
|
|
||
|
|
Alors k = 2n |
|
Voir Nombres
en puissance de 2
|
Les nombres en 2k
+ 1 |
|
|
|
Observation
|
En jaune les nombres premiers |
|
|
Domaine
pour N = 2k +1
|
|
|
|
|
||
|
Tout diviseur premier
de Fn est de la forme: 2n+1 . k + 1 Exemple |
||
|
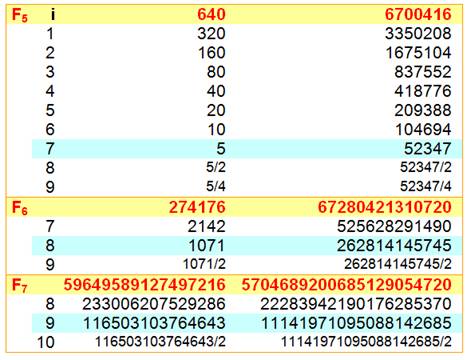
F5 641 6 700 417 |
= 641 x 6 700 417 = 64 x 10 + 1 = 2 5+1 x 10 + 1 = 64 x 104694 + 1 |
|
|
Analyse
Exemple |
||
|
640 / 21 640 / 22 … 640 / 27 |
= 320 = 160 = 5 |
|
|
Ce diviseur de F5 est divisible par 27 et 7 = 5 + 2. Exploration
Généralisation Tout diviseur de Fn est de la forme: 2m k + 1, avec k impair et m
|
||
|
FERMAT & MERSENNE |
|
|
|
Un nombre de Fermat
n'est jamais produit de deux nombres de Mersenne. Fx
22^x + 1 Démonstration |
||
|
La démonstration est effectuée dans le
monde du modulo 3. |
Si la situation est impossible en modulo 3, elle l'est a fortiori
sans modulo. |
|
|
Calcul sur le nombre de Fermat. |
22^x +
1 = 22t + 1 = (2²)t + 1 = 4t + 1 |
|
|
Modulo 3. |
|
|
|
Alors que pour Mersenne, le modulo vaut 0
pour x pair et 1 pour x impair. |
2x – 1 2y – 1 |
|
|
Et, pour le produit des deux nombres de
Mersenne: |
(2x –
1) (2y – 1) |
|
|
En rapprochant les deux résultats: |
Égalité jamais possible |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Fermatdi.htm |
![]()