NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/01/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	PUISSANCE de 2
Débutants Puissance	Nombres de Fermat et Mersenne				Glossaire Puissance
INDEX Puissance Décomposition Puissance de 2 Nombres en puissance		FERMAT (biographie)		MERSENNE (biographie)
		Nombres de Fermat		Nombres de Mersenne
		Valeurs et facteurs		Valeurs et facteurs
		Voisins premiers		Voisins premiers
		Diviseurs		Mersenne composés
				Carol et Kynea
				Williams
	Sommaire de cette page >>> Propriété fondamentale >>> Nombres de Mersenne >>> Exposant premier >>> Théorèmes et conjectures >>> Mersenne en puissance		>>> Mersenne et diviseurs >>> Mersenne & Mersenne – 1 >>> Compagnons des nombres de Mersenne >>> Historique >>> Mersenne – Biographie

NOMBRES de MERSENNE

M_n = 2ⁿ – 1

Puissance de deux moins un.

Intérêt particulier porté sur les nombres de Mersenne premier.

Note: Généralement un nombre de Mersenne est entendu comme un nombre de Mersenne premier.

Les nombres de Mersenne sont un cas particulier des nombres de Cunningham et également des nombres de Williams.

En bref

Propriétés fondamentales
Si on connaît un nombre de MERSENNE premier: 2^n – 1	Alors, on connaît un nombre PARFAIT beaucoup plus grand: 2^n – 1 (2^n – 1)

Voir Défi de Frénicle à Fermat

NOMBRES DE MERSENNE (1664)
Théorème Mn = 2^n – 1 Si ce nombre est premier alors n est premier. La réciproque n'est pas vraie.	Exemples M2 = 2² – 1 = 3 C'est le N°1 M3 = 2^3– 1 = 7 C'est le N°2 M5 = 2^5– 1 = 31 C'est le N°3 Voir Liste des nombres de Mersenne et Record des nombres de Mersenne premiers
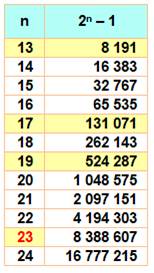
Exploration de ce théorème Pour ces nombres premiers, 2^n – 1 est composé: 11, 23, 29, 37, 41, 43, 47, 53, 59, 67, 71, 73, 79, 83, 97, 101, 103, 109, 113, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199 …	Liste pour les premières valeurs Suite de ce tableau
Repunit en binaire Cas des rep-units, nombres formés de 1, en binaires. Traduit en décimal, ce sont tous des nombres de Mersenne.	112 = 310 = 4 – 1 = 2^2 – 1 1112 = 710 = 8 – 1 = 2^3 – 1 11112 = 1510 = 16 – 1 = 2^4 – 1

Démonstration express

2ⁿ – 1 , si n est composé, il peut s'écrire 2^km – 1 et se factoriser en:

2^km – 1 = (2^k – 1) (2^{k (m-1)} + … + 2^kl + 2^k + 1).

Donc n est composé, et 2ⁿ – 1 ne peut pas l'être (car divisible par 2^k – 1.

2ⁿ – 1 ne peut être premier que si n l'est.

Il s'agit ici d'une démonstration par l'affirmation opposée, dite par contraposée.

On peut même démonter que: si a et n sont des entiers plus grand que 1, si aⁿ – 1 est premier, alors a = 2 et n est premier.

Voir Divisibilité des nombres de Mersenne / Contraposée

Exposant premier
N = a^n – 1 Ce nombre n'est premier que si a = 2 et n est premier, et c'est justement un nombre de Mersenne. Démonstration
Calcul avec le développement:	a^n – 1 = (a – 1) (a^n-1 + a^n-2 + … + a + 1)
Pour être premier l'un de ces deux facteurs doit être égal à 1. Or le deuxième est > 1. C'est donc le premier qui vaut 1.	(a – 1) = 1 a = 2
Supposons que n soit composé Avec r et s > 1	n = r . s
Nouveau calcul: Le nombre est alors le produit de deux facteurs. Chacun est > 1. Il est composé et non premier comme le veut l'hypothèse.	a^n – 1 = 2^rs – 1 = (2^r – 1) (2^r(s-1) + 2^r(s-2) + … + 2^r + 1)
Seule possibilité	2^n – 1 est premier que si n est premier

THÉORÈMES ET CONJECTURES

On ne sait pas prouver que: Les nombres de Mersenne premiers sont en nombre infini. Les nombres de Mersenne composés, ayant un exposant premier, sont en nombre infini. On sait aujourd'hui que: Si Mp est premier, alors p l'est aussi, mais la réciproque n'est pas vraie. Par contre: si p est composé alors Mp est composé (Connu de Mersenne) – Voir Démonstrations Les nombres de Mersenne sont premiers entre eux. C'est la base d'une démonstration montrant qu'il existe un nombre infini de nombres premiers. Chaque nombre de Mersenne engendre un nombre parfait Euler a montré que: Si k > 1 et p = 4k + 3 est premier, alors 2p + 1 est premier si et seulement si 2^p = 1 (mod 2p+1). Donc, si p = 4k + 3 et 2p + 1 sont premiers alors le nombre de Mersenne 2^p– 1 est composé.  Il semble raisonnable d'affirmer qu'il y a une infinité de telles paires p et 2p+1. Conjecture La nouvelle conjecture de Mersenne, Bateman, Selfridge et Wagstaff affirme que: Soit p un entier impair quelconque. Si deux des conditions suivantes sont remplies, alors la troisième aussi : 1) 2) 2^p- 1 est premier (un premier de Mersenne, évidemment) 3) (2^p+ 1)/3 est premier. Vérifiée pour tous les premiers p < 100 000.

MERSENNE en puissance
Est-ce que ces nombres sont premiers?	= 170141183 4604692317 3168730371 5884105727 C5 > 10^5121759971936968187987972338633157624
Selon Dickson, Catalan répondit en 1876 à Lucas, en affirmant que C4 = 2^127 - 1 est premier. Il est improbable que tous ces nombres soient premiers. C'est un exemple de la grande loi de Guy sur les petits nombres.

Voir Nombres Sublimes

MERSENNE et diviseurs
Observons la somme des diviseurs des nombres de Mersenne premiers. Et leur produit.	M2 = 2^2 – 1 = 3 = 1 + 3 = 4 = 2^2 M3 = 2^3 – 1 = 7 = 1 + 7 = 8 = 2^3 M5 = 2^5 – 1 = 31 = 1 + 31 = 32 = 2^5 = 2^2 . 2^3 = 2^5 = 32 = 2^2 . 2^3 . 2^5 = 2^10 = 1024
Si Mp = 2^p – 1 Produit de nombres de Mersenne premiers: la somme des diviseurs est égale à 2 à la puissance de la somme des indices:

Voir Nombres sublimes (propriété utilisée pour la démonstration)

MERSENNE & M – 1 = 2^n – 2 = 2(2^n-1 – 1)
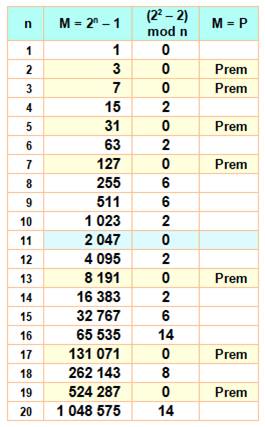
Propriété amusante avec un nombre de Mersenne Mn et Mn – 1. On pourrait penser que si Mn – 2 est divisible par n, alors le nombre de Mersenne est premier. Ex: M5 = 2^5 – 1 = 31 qui est premier et 30 = 5 x 6 (en jaune sur le tableau). Hélas, ça ne marche pas toujours. Ex: M11 = 2^11 – 1 = 2 047 = 23 x 89 et 2046 = 11 x 186 (en bleu sur le tableau). Pire, la quantité de faux augmente. Pour n jusqu'à 100 10 Vrais: [2, 3, 5, 7, 13, 17, 19, 31, 61, 89] 16 Faux: [1, 11, 23, 29, 37, 41, 43, 47, 53, 59, 67, 71, 73, 79, 83, 97] Pour n jusqu'à 1000 14 Vrais: […, 107, 127, 521, 607] 158 Faux: […, 101, 103, 109, 113, 131, 137, 139, 149, …] Pour n jusqu'à 10 000 20 Vrais & 666 Faux	Cette affirmation est fausse

Voir Nombre 666

Compagnons des nombres de Mersenne					haut
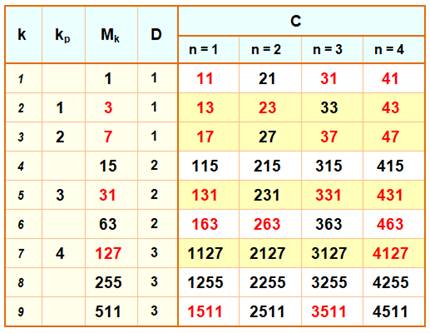
Définition des nombres compagnons Ce sont des nombres premiers de la forme: Ck = Mk + n × 10^D Avec D, la quantité de chiffres dans le nombre de Mersenne. Lecture du tableau k est le rang du nombre de Mersenne et kp celui du nombre premier. Mk est le nombre de Mersenne. D est la quantité de chiffre de Mk. C est le nombre compagnon selon le coefficient n. En rouge, les nombres premiers.			Exemples
Compagnons premiers On ne conserve que les nombres de Mersenne premiers. Parmi, les nombres premiers qui restent, on note le premier en tête. C'est le nombre compagnons de Mersenne.			Tableau réduit aux nombres premiers
Liste 1: valeur de n suivi du nombre de Mersenne Liste 2: valeur de n pour les Mersenne premier successifs	[1, 3], [1, 7], [1, 31], [4, 127], [1, 8191], [10, 131071], [1, 524287], [36, 2147483647], [15, 2305843009213693951], [58, 618970019642690137449562111], … 1, 1, 1, 4, 1, 10, 1, 36, 15, 58, 57, 55, 310, 177, 51, 2389, 973, 532, 1750, 63, 1032, 1240, 3757, 9994, 5854, 12870, 46147, 11923, 17113, 10296, 5977, … Voir OEIS A209985 – Values of the first prefixing digits for Mersenne primes Voir OEIS A202136 – Prefixing digits to Mersenne primes to obtain larger primes Auteur: Gil Mozzo
Quantité de nombres premiers pour chaque Mersenne pour n de 1 à 100		41, 45, 30, 21, 22, 14, 13, 9, 5, 3, 1, 3, 0, 0 … Lecture: entre n = 1 à 100, il y a 41 nombres premiers de type C. La densité tend vers 0 pour les grands nombres de Mersenne.
Programme Maple				But Lister les valeurs de n pour les compagnons Mersenne successifs. Commentaires Ouverture de la liste L. Calcul de M et de sa quantité de chiffres via le logarithme. Balayage en n et calcul du compagnon potentiel P. S'il P est premier et M est premier, ajouter la valeur de n à la liste. Arrêt du balayage (break) en n dès qu'un P premier a été trouvé. On ne cherche que le plus petit n. Impression de la liste L en fin de programme.
Listing du programme pour copier-coller restart: L := []: for k from 2 to 100 do M := 2^k-1; d := floor(log[10](M))+1; for n to 1000 do P := n*10^d+M; if isprime(P) and isprime(M) then L := [op(L), n]; break end if end do end do: L;

Voir Compagnons des nombres de Fermat / Programmation – Index

Idée de Gil Mozzo que je remercie pour ce partage d'informations

HISTORIQUE

Avant De nombreux auteurs pressentaient que les nombres de la forme 2^n – 1 étaient tous premiers Regius – 1536 Hudalricus Regius montre que 2^11– 1 = 2 047 n'est pas premier (2 047 = 23 x 89).  Cataldi – 1603 Pietro Cataldi vérifie que 2^17– 1 and 2^19– 1 sont tous les deux premiers, mais indique faussement que 2^n– 1 est aussi premier pour 23, 29, 31 et 37.  Fermat – 1640 Fermat montre que Cataldi avait tort pour 23 et 37. Arrive le moine français Marin Mersenne (1588-1648) Mersenne mentionne dans la préface de son livre Cogitata Physica-Mathematica (1644) que le les nombres 2^n- 1 sont premiers pour : n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 et 257 et qu'ils sont composés pour les autres n < 257.  La conjecture, incorrecte, de Mersenne était à peine meilleure que celle de Regius, mais c'est son nom qui reste attaché à ces nombres.  Les cinq erreurs de Mersenne n'ont été résolues définitivement qu'en 1952 par Robinson par ordinateur. Euler – 1750 Euler montre que Cataldi avait tord aussi pour 29 et raison pour 31.   Lucas – 1876 Après un siècle, Lucas vérifie que 2^127- 1 est premier aussi.   Il a mis au point un test de primalité des nombres de Mersenne, amélioré par Lehmer en 1930. Application à la main pour les 19 premiers Mersenne (p < 258). Pervusin – Sept ans plus tard Il montre que 2^61- 1 est premier. Mersenne n'avait pas vu celui-là.  Powers – Au début des années 1900 Il montre que Mersenne était passé à côté de 2^89- 1 et 2^107- 1  Finalement, en 1947 La liste correcte des nombres de Mersenne pour n < 258, est établie et vérifiée : n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 et 127 Depuis, avec les ordinateurs En 195, M257 est confirmé en quelques secondes sur la machine SWAC. Avec la capacité croissante des ordinateurs, sans oublier de réel progrès en technique de calcul (factorisation et test de primalité), les records tombent régulièrement et, en fait, donnent les plus grands nombres premiers connus.

Un beau spécimen

2⁵²¹ – 1 = 512 2⁵¹² – 1

= 6,8648 … 10¹⁵⁶

Premier de Mersenne et de Woodall

(Trouvé par Dobb, cité par Caldwell)

Voir Nombres premiers de Woodall

Père Marin Mersenne (1588-1648 : 60 ans)

Sa vie Savant, philosophe français né à Oizé près du Mans. Collège des jésuites de la Flèche (comme et avant Descartes). En 1611, religieux de l'ordre des Minimes dans un couvent situé à l'actuelle place des Vosges (Paris). Nevers, enseignement de la philosophie. En 1619, il rejoignit Paris, et entra au couvent de l'Annonciade. Ami et correspondant de Descartes et de nombreux autres savants: Huygens, Fermat, Hobbes. Il crée autour de lui une activité philosophique et scientifique. En 1635, il organise des réunions régulières, sorte d'académie: Roberval, le père de Pascal (Étienne) … Ce foyer de réflexion animé par Mersenne conduira à la création par Colbert de l'Académie des sciences en 1666. 1636: De l'harmonie universelle, traité d'acoustique physique et mathématiques des instruments de musique. 1644-1645, en Italie: découvre le baromètre et le fait connaître en France, notamment à Pascal. Son œuvre Il détermine les rapports des fréquences des notes de la gamme. Il mesure la vitesse du son (1636). Connu pour les nombres qui portent son nom.

Suite et Retour	Mersenne – Suite Mersenne composés Mersenne – Table des nombres et records Mersenne généralisés Fermat Nombres sublimes
Voir	Carrés Magiques Géométrie – Index Humour – Index Jeux – Index Nombres magiques Rubriques débutants Théorie des nombres Tous les types de premiers
Site	OEIS A001348 – Mersenne numbers Mersenne numbers – Guy Haworth – Intérêt historique

Pages voisines: Nombres Remarquables

Puissance 2		Fibonacci	Nombres Kaprekar
Fermat	Mersenne	Pascal	Nombres Chanceux	Nombres d'Euler
Parfait	Sublime	Catalan	Nombres Poulet	Nombres Têtus

Suite en Autres noms de nombres 

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Mersenne.htm