Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 06/04/2024 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Quart de cercle	Deux cercles et rectangle
	Fourmi sur un pavé	Cinq cercles (arbelos)	Trois cercles tangents
	Cercle sur équerre	Cercle et trois points	Quatre cercles et un quart

Quatre cercles plus un dans un carré Quel est le rayon du petit cercle central ?
	Sommaire de cette page >>> Quatre cercles dans le carré	Débutants Géométrie Glossaire Géométrie

Devinette

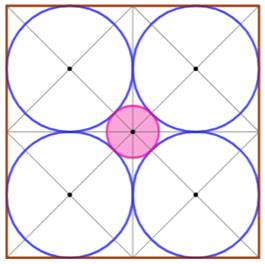
Une urne (rose) est dessinée à partir de quatre cercles identiques, de rayon unité, tangents trois à trois. Quelle est l'aire de l'urne ?

Solution / Brève 53-1048

Quatre cercles dans le carré		haut
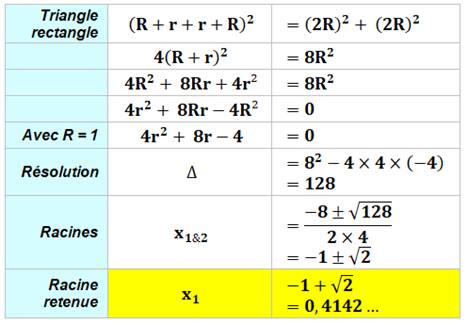
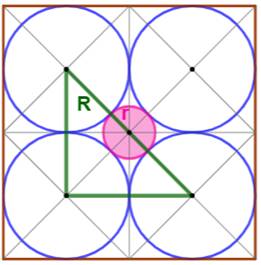
Construction Quatre cercles sont inscrits dans les quadrants d'un carré de côté 4. Un cercle rose est tangent à ces quatre cercles. Quel est son rayon? Solution (Figure du bas) On connait le rayon des quatre cercles: 4/4 = 1. Avec le théorème de Pythagore dans le triangle rectangle vert:

Figure et mesures avec GeoGebra

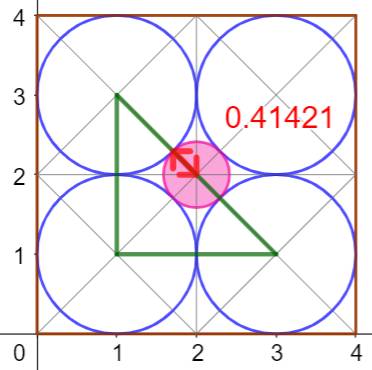
Voir GeoGebra

Devinette – Solution

Construction Une urne (rose) est dessinée à partir de quatre cercles identiques, de rayon unité, tangents trois à trois. Quelle est l'aire de l'urne ? Solution (figure du bas) L'épure du dessin montre que les centres des cercles forment un carré. L'urne est formée d'un disque posé sur un pied qui est la zone centrale des quatre cercles. Celle-ci est la partie évidée du carré lorsqu'on lui retire quatre quarts de cercle (soit un cercle). Aire de l'urne = (Aire du carré – Aire disque) + aire disque = Aire du carré = 4. L'aire de l'urne rose est égale à celle du carré.

Retour / Autres énigmes

Haut de page

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Nappe sur table Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/QuatCerc.htm