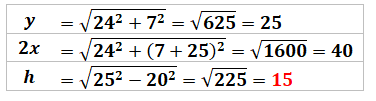|
Édition du: 14/01/2024 |
|
INDEX |
Théorème de Pythagore |
|||
![]()
|
Théorème de Pythagore Débutants – Novices Page de
découverte pour jeunes enfants ou pour novices. Ce théorème, comme celui de
Thalès, est omniprésent dans toute la scolarité, collège comme lycée et
même ensuite. Il donne
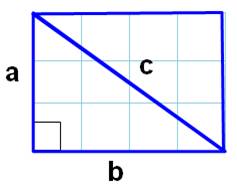
la mesure de la diagonale d'un rectangle,
ou encore celle du grand côté d'un triangle
rectangle. |
||
|
et collège |
Sommaire de cette page >>> Théorème de Pythagore – Visuel >>> La découverte de Pythagore >>> Une découverte universelle >>> La preuve >>> Et avec d'autres unités de mesure? >>> Hypoténuse en escalier >>> Application du théorème de Pythagore >>> Le triangle dans le carré |
Débutants Glossaire |
Voir aussi Le diaporama de Clément (9 ans) /
Toutes les pages
débutants
|
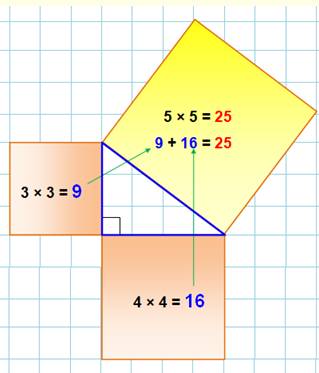
Sur
ce dessin, comptez les billes:
Vous
remarquez qu'il y a 9 + 16 = 25 billes rouges et oranges, donc autant que de
billes vertes. ROUGES + ORANGES = VERTES
en quantité de billes. |
|
|
|
Pythagore
dessine des triangles rectangles, il découvre un joli triangle dont les trois
côtés ont des longueurs entières en cm. Ça tombe
bien! Pythagore adore les
nombres entiers. |
Un triangle
magnifique: que des nombres entiers pour
la longueur des côtés. En plus, son aire est égale à 6 et son
demi-périmètre à 7.
Il est sacré. |
|
|
Il a l'idée de comparer les carrés qu'il a
dessinés à partir des trois côtés. Il calcule l'aire de chacun.
Stupéfaction,
l'aire du grand est égale à celle du petit ajoutée à celle du moyen: 9 + 16 = 25 En
reprenant le calcul: 3x3 + 4x4 = 5x5 On écrit
avec la notation des carrés par un petit 2 en haut (on dit: en exposant) : 3² + 4² = 5² |
Surface du jaune
= surface des deux en marron |
|
|
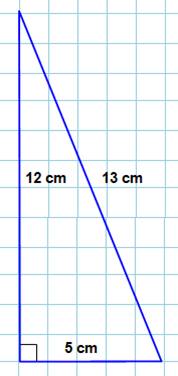
Pythagore
continue ses recherches et découvre de nombreux autres triangles avec des
nombres entiers comme longueurs des côtés. La figure
montre un nouvel exemple pour lequel on vérifie encore: 5² + 12² = 13² 5x5 + 12x12 = 13x13 25 + 144 = 169 |
|
|
|
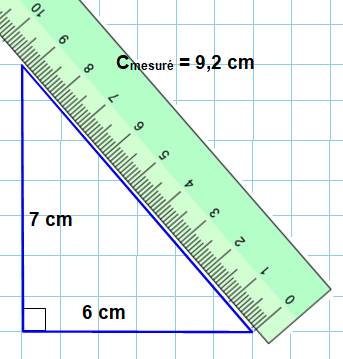
Cette fois, il veut en avoir le cœur net! Il
dessine un triangle avec 6 cm et 7cm pour deux des côtés et il mesure le
troisième. Pas de chance, ça ne tombe pas juste! Il mesure
9,2 cm. Il vérifie tout de même avec les carrés 6² + 7² = 6x6 + 7x7 = 36 + 49 = 85 9,2 x 9,2 = 84,64 Eh! Pas loin! Il n'a pas de calculette, mais vérifie tout de
même que le nombre qui au carré donne 85 est plutôt: 85 = 9,22 x 9,22 Évidemment
pas possible de mesurer avec cette précision avec sa règle. |
|
|
Voir Découverte
du nombre qui multiplié par lui-même donne 2 (racine de 2)
|
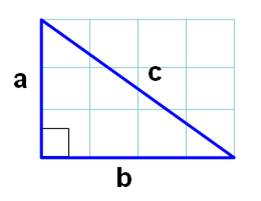
Pythagore
trouve une preuve géométrique qui indique que: Pour tout
triangle rectangle: Le grand côté c est appelé l'hypoténuse. Alors,
on énonce: Pour tout triangle rectangle, le carré de
l'hypoténuse est égal à la somme des carrés des deux autres côtés. Note: si on était exigeant, on dirait: le carré de la longueur de l'hypoténuse est égal à la somme des
longueurs des carrés des deux autres
côtés. |
Le théorème ou la relation de Pythagore permet le calcul de la
longueur de l'hypoténuse du triangle rectangle mais aussi la longueur de la
diagonale du rectangle,
comme celle du carré
d'ailleurs.
|
|
|
Une des
démonstrations possibles est illustrée par cette figure. Avec quatre triangles rectangles identiques
(bleus) et les deux petits carrés (jaunes), on forme le grand carré de
gauche. Pour
former la figure de droite, on retire les deux carrés jaunes, libérant un
espace dont l'aire vaut a² + b². Tout en restant dans le même grand carré, on fait
glisser les quatre triangles dans les coins. L'espace central est un carré de
côté c et son aire est c². Ainsi, l'espace libéré (a²
+ b²) a la même aire que le carré c². |
Les carrés en a² et b² occupent la même
surface que le carré en c². |
|
|
Pour les curieux Le quadrilatère
noté c² est bien un carré
! |
Ce quadrilatère a ses quatre côtés égaux à la longueur de l'hypoténuse
des triangles rectangles qui sont tous égaux. C'est un losange. Voyons l'angle au sommet. Il est entouré de deux angles bleus qui sont
en fait les deux angles d'un triangle
rectangle. Leur somme vaut 90° (ils sont complémentaires). L'angle au
sommet du losange vaut 180 – 90 = 90° (un angle droit). Un losange avec un angle droit est un carré. |
|
Peut-être
un moyen pour retenir ce mot étrange

Hippopotamus est l'hippopotame en
latin et en anglais
Rappel pour l'orthographe; hippos = cheval et potamos
= le fleuve
Le dessin est de![]()
|
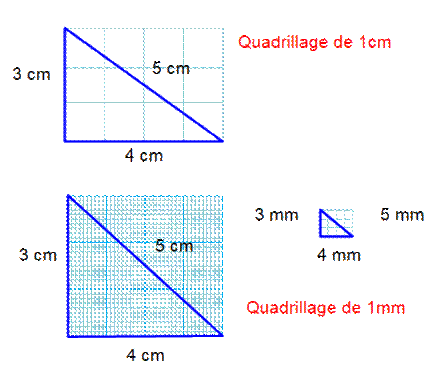
Et si je
dessine un quadrillage plus petit; de plus en plus petit. Que se passe-t-il? Avec le même triangle dans un quadrillage plus
fin, évidemment les longueurs ne changent pas et la relation de Pythagore est
toujours valable (figures de gauche). Si le triangle est plus petit (figure de droite), le théorème de
Pythagore s'applique toujours, seulement ce ne sont pas les mêmes unités. |
|
|
Pourquoi cette remarque sur les unités de mesure
|
Plusieurs
fois la question m'a été posée: si je mesure l'hypoténuse en suivant le
quadrillage, j'ai l'impression que ça change les choses. Les marches de
l'escalier deviennent de plus en plus petites. Voyons
cela … |
|
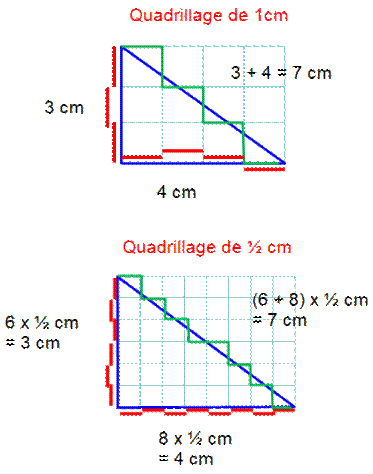
Quelle
est la longueur de l'hypoténuse si je la parcours le long des lignes du
quadrillage? Oups!
Attention, la ligne verte de la figure n'est pas l'hypoténuse! C'est la
descente d'escalier. On peut
compter les segments verts: il y en a 7, soit une longueur de 7 cm. Plus
simple:
Même en
prenant un quadrillage plus petit (Figure
en bas):
|
Dans tous
les cas, la longueur de l'escalier vert est égale à la longueur des segments
rouges, et donc, à la longueur des deux côtés du triangle. |
|
Voir
aussi:
Problèmes
du même type posée en CM2
Ne pas confondre
|
La
longueur de l'hypoténuse n'est en aucun cas la longueur de l'escalier qui décrit
l'hypoténuse en suivant le quadrillage. Oui
mais, si le quadrillage devient infiniment fin. Alors, là, on cherche les
ennuis. On s'approche d'un
paradoxe. |
|
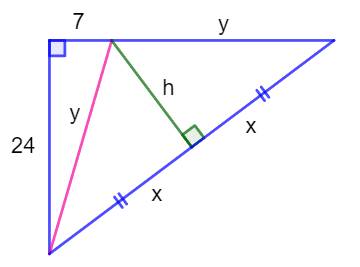
Construction Un
triangle rectangle dont l'un des cotés mesure 24 cm. La
médiatrice
de l'hypoténuse coupe l'autre côté du triangle à 7 cm de l'angle droit. Quelle
est la longueur h du segment de médiatrice ? Piste (Figure
du bas) On
trace le segment rose, qui du fait de la médiatrice, a une longueur égale à
y. Avec
une succession de "Pythagore",
il est très facile de calculer successivement y, x et enfin h. Une
chance, les données ont été choisies pour produire des triplets de
Pythagore (valeurs en nombres entiers) Calculs
Le segment de médiatrice mesure h = 15 cm.
|
|
|
Voir Défis géométriques
|
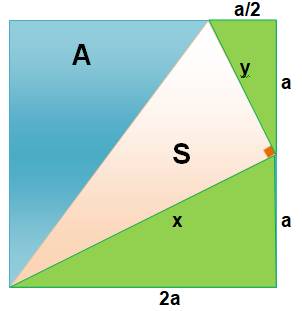
Construction (Figure
du haut) Un
triangle rectangle est inscrit dans un carré de côté 2a. Un
sommet commun avec le carré et un sommet au milieu d'un côté du carré. Quelle
est l'aire S du triangle en fonction de l'aire A du carré ? Piste (Figure
du bas) Les
deux triangles verts sont semblables dans un rapport 1/2 (les trois angles
sont égaux deux à deux). Alors,
le petit côté du petit triangle vaut a/2. On
calcule la longueur de l'hypoténuse de chaque triangle (x et y) en appliquant
le théorème de Pythagore. L'aire
du triangle rectangle est S = 1/2 xy. Calculs
|
|
|
Merci à Thierry P. qui, par ses questions,
m'a amené à composer cette page pour novices
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThPythDb.htm
|
![]()