|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Récréations mathématiques Énigme du chameau et des bananes Aussi avec dromadaire, éléphant; pommes. Le chameau dans le désert, la traversée du désert,
Énigme Einstein 2. Énigme, sous divers noms, archi-classique et qui
donne bien du fil à retordre si on ne connait pas la solution.
Deux types de questions: quelle est la distance maximale parcourue par le
chameau, ou quelle est la quantité de bananes disponibles à une distance
donnée? |
Voir Énigme d'Einstein
Amuse-bouche
|
Quelle distance maximum peut parcourir un
chameau qui peut porter 3 bananes, en consomme une par kilomètre, avec un
stock de 6 bananes au départ? Le chamelier crée un dépôt au premier kilomètre. Il y
dépose 1 banane tout en ayant consommé 2 bananes pour effectuer
l'aller-retour. De retour à son point de départ, il prend les 3 bananes
restantes, en consomme 1 pour rejoindre le dépôt; prend celle du dépôt et
avec ces 3 bananes parcourt 3 km. Total 4 km d'autonomie pour ce chameau. |
Vocabulaire
|
Entre le départ et
la destination, le chamelier crée des dépôts de bananes. Le parcours complet est ainsi
constitué de tronçons. Sur chaque tronçon,
le chameau exécute des allers-retours (A/R)
en un certain nombre de trajets. La distance maximale parcourue par le chameau avec son
stock initial de bananes est son autonomie.
|
![]()
|
|
||
|
Le défi Avec un stock de 3 000 bananes,
comment en transporter un maximum sur 1 000 km avec
un chameau qui ne peut en porter que 1 000 à la fois
et qui en consomme une à chaque kilomètre ? |
||
|
Données Distance: 1 000 km Stock au départ: 3 000 km Consommation: 1 banane / km Notes Le parcours est en ligne droite. Le chameau a besoin de manger sa banane tout au
long du kilomètre parcouru. |
Exploration de quelques possibilités 1) Si le chameau pouvait transporter les 3 000 bananes, il en
mangerait 1 000 sur le parcours; soit 2 000 à destination. 2) Avec un chargement complet de 1 000 bananes, le chameau parcourt
les 1 000 km, mais tout le chargement est englouti. Rien à destination et
impossible de retourner (Illustration –
Scénario 1). 3) Avec 1 000 bananes sur les dos, il peut aussi faire 500 km puis
revenir. Voyage inutile, car il a tout mangé pour se retrouver au point de
départ (Illustration – Scénario 2). |
|
|
Illustration
|
||
|
Déductions |
4) Le dromadaire doit constituer un dépôt de bananes à moins de 500 km
de son départ. 5) Pour rentabiliser le trajet, mieux vaut que le dromadaire soit
systématiquement chargé de ses 1 000 bananes. |
|
|
|
|
|
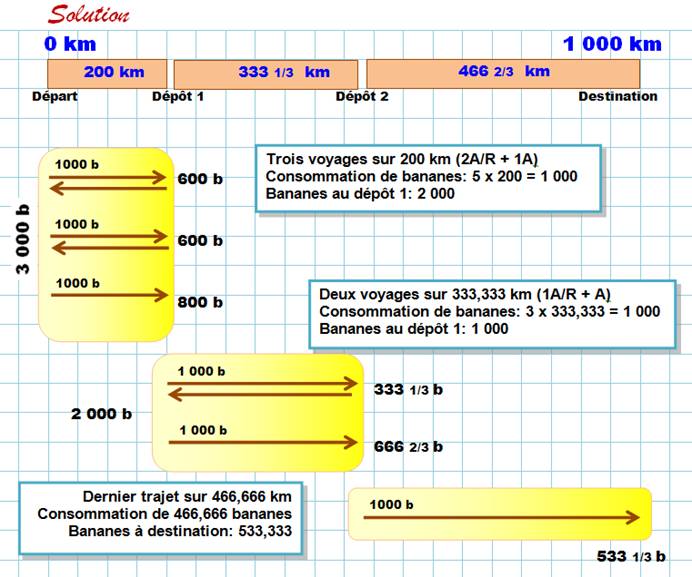
La
solution comporte la constitution de deux dépôts (trois tronçons), l'un à 200
km du point de départ et l'autre à 333,333 km du premier dépôt (Voir illustration ci-dessous).
|
|
|
|
|
|
|
||
|
k = 100 On forme
des dépôts de bananes tous les 100 km et voyons combien de bananes sont
livrées à destination. Tant que
le dépôt contient plus de 2 000 bananes, cinq trajets sont nécessaires. Dès que le
dépôt en contient moins de 2 000, trois trajets suffisent. Et avec
moins de 1 000, un seul trajet suffit à porter toute la cargaison. Colonne 1: distance
parcourue. Colonne 2: consommation de
bananes (C). Colonne 3: bananes au dépôt. |
|
|
|
k = 1 En
augmentant la quantité de dépôts, la quantité de bananes sauvées à l'arrivée
est plus importante. Deux remarques importantes 1) Le dernier
dépôt avec moins de 1000 banane autorise un seul trajet. 2) Dans
les deux cas étudiés, le premier dépôt est toujours à 200 km. Il est
atteignable en 2 A/R et 1 A avec une charge de 1000 au départ. Inutile de multiplier les A/R. |
|
|
|
|
||
|
Premier tronçon Pour
profiter à plein des capacités du chameau, il doit transporter les 3000
bananes en trois voyages (5 trajets). Note: On se souvient que le chameau
ne peut pas faire plus de 500 km A/R; alors, il aurait consommé toutes les
bananes transportées. |
Si le point D1 est à la distance x du
départ, la consommation est égale à 5x et la quantité de bananes livrée en D1
est 3000 – 5x. Le mieux est de profiter encore de ce maximum à partir du prochain
dépôt; donc, de laisser 2000 bananes en D1: 3000 – 5x = 2000 => x = 200 km |
|
|
Deuxième tronçon Toujours
pour l'optimum, à partir du premier dépôt, le chameau doit faire 2 voyages (3
trajets). Note: Compte tenu des consommations
(5, 3, 1), il est clair que les distances doivent être dans l'ordre inverse:
courte, moyenne et grande. |
Si le point D2 est à la distance y du
dépôt précédent, la consommation est égale à 3y et la quantité de bananes
livrées est 2000 – 3x.
2000 – 3x = 1000 => y = 333,333 km |
|
|
Troisième tronçon Le trajet
s'effectue en un seul trajet Note: Certains n'acceptent pas les
tiers de bananes et donnent la solution: 533 avec (200, 333, 667 km). |
Distance entre D2 et destination: 666,666 km Des 1000 bananes en D2, il ne restera que 533,333
bananes à destination. |
|
|
|
||
|
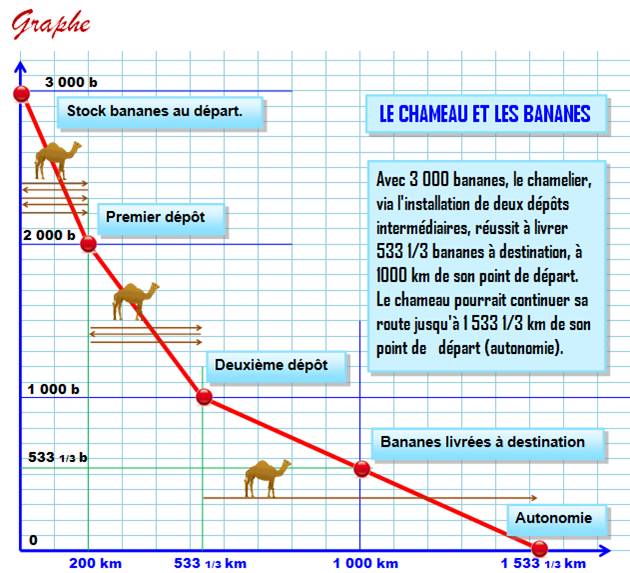
Notations (valeur
numérique de notre exemple) Stock de
bananes : B = 3 000. Capacité
d'emport: C = 1000. Distance
à parcourir: D = 1000 km Consommation:
1 banane / km Quantité
de tronçons: |
Consommation Pour profiter au maximum des capacités d'emport, le chameau consomme,
en fonction de ses A/R:
|
|
|
Si q est une valeur entière Distance
maximale que le chameau peut parcourir. On tire
parti du maximum pour chaque dépôt. En
reprenant notre exemple, le chameau pourrait parcourir 1533,333 km en
consommant toutes les bananes. Si on
l'arrête à 1000 km, il lui restera 533,333 bananes. |
Formule
Notre exemple
|
|
|
Si q n'est pas une valeur entière Distance maximale
que le chameau peut parcourir. |
|
|
Merci à Pierre Pardo pour
ses remarques
Voir Géographie
– Index
|
|
||
|
Camel and bananas Monkey and sand Boy carrying watermelons Jeep problem Exploration problem |
A camel must travel 1000
kilometers across a desert to the nearest city. She has 3000 bananas but can
only carry 1000 at a time. For every kilometer she walks, she needs to eat a
banana. What is the maximum number of bananas she can transport to the city? |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()