|
||||||||||||||||||||||||||||||||
![]()
|
Inéquations Pas très compliqué, mais un
piège nous attend … vite déjoué! |
Voir aussi Initiations
aux Opérations arithmétiques
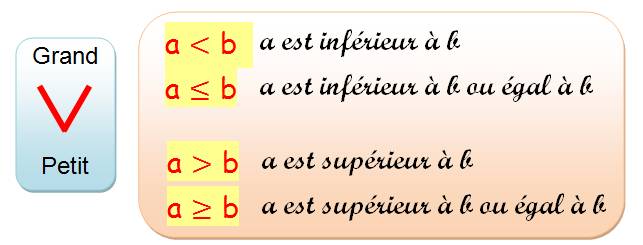
Notations
|
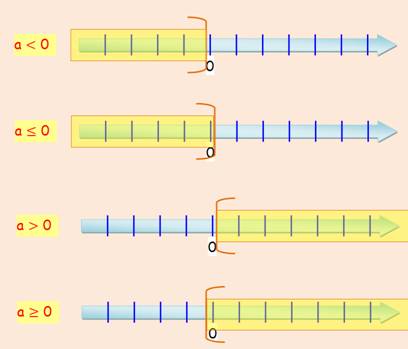
Représentation sur la droite graduée
|
|
|
|
|
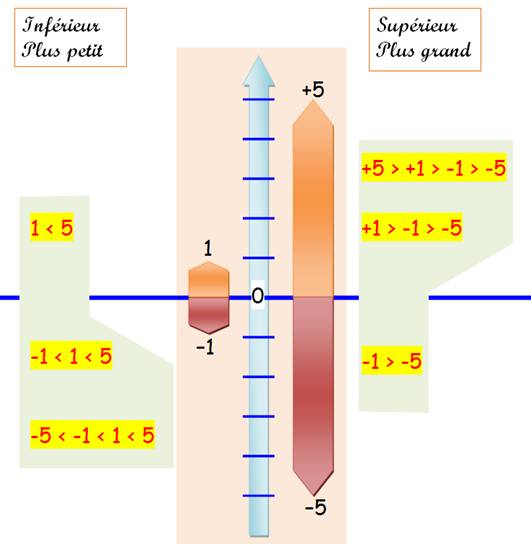
Prenons quatre nombres et comparons-les.
Notez cette bizarrerie: Le nombre 1 est inférieur à 5, mais – 1 est supérieur à – 5. Mais, ce phénomène est tout à fait évident en regardant
le graphique. La grande barre horizontale du zéro agit comme une
espèce de miroir dans lequel tout s'inverse
|
|
Absolu et relatif
|
Les
nombres avec un signe sont des nombres
relatifs. Si
leur signe est éliminé, on dit que l'on prend leur valeur
absolue. |
|
|
||
|
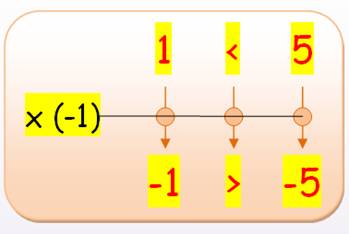
Voyons cet effet miroir où tout s'inverse, les signes: Les nombres devenant négatifs, l'inégalité change de
sens. Transformer du positif en négatif, c'est multiplier les
nombres par (– 1). Et Inversement. |
|
|
|
Le même effet d'inversion se produit en partant de
nombres négatifs. Souvenez-vous que pour la multiplication: "moins
par moins donne plus" >>> |
|
|
|
Même si les deux sont négatifs. Inégalité réciproque de la première. |
|
|
|
Généralisation Multiplier une
inégalité par un nombre négatif, inverse le
sens de l'inégalité. Notez que comme dans les égalités, les deux côtés
doivent être traités de la même manière.
Si on multiplie à gauche, il faut multiplier de la même quantité à droite. Exemple 2a + 5bc > d Multiplication par
-5 – 10a – 25bc < – 5d |
|
|
|
||
|
Résoudre une inéquation consiste à trouver le domaine de
valeurs de l'inconnue x. |
x
> 6 x
|
|
|
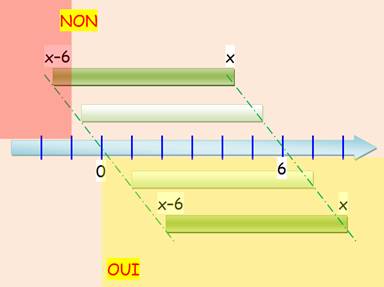
Comme dans les équations, l'inconnue est enfouie dans
une relation qu'il faut démêler. L'illustration montre une barre qui
représente la longueur: x – 6. Lorsque cette barre se déplace, trois cas
se présentent:
La solution de cette inégalité est x > 6. |
x
– 6 > 0 x
– 6 + 6 > 0 + 6 x
> 6
|
|
|
|
||
|
Nous venons de le voir, nous pouvons additionner de
chaque côté et procéder comme pour les
équations. |
|
|
|
Addition et soustraction: ça marche |
Si
a > 5, alors: a + 1000 > 5 + 1000 a
– 1000 > a – 1000 |
|
|
Multiplication et division
par un nombre positif: ça marche |
Si
a > 5, alors: 1000a
> 5 0000 a
/ 1000 > 5 / 1000 |
|
|
Multiplication et division
par un nombre négatif: ça marche en
renversant |
Si
a > 5, alors: –2a
< –10 –a
/ 3 < – 5 / 3 |
|
|
Attention à ne pas diviser
par 0 |
Si
a > 5, alors: a
/ (b – c) > 5 / (b – c) que si b |
|
|
À noter Permutation des membres de l'inéquation, c'est possible
en faisant suivre le sens. |
18 > 3x + 7 3x
+ 7 < 18 |
|
|
|
|||
|
Pas à pas |
2x + 2 2x + 2 – x x + 2 x + 2 – 2 x |
>
x + 5 >
x + 5 – x >
5 >
5 – 2 >
3 |
|
|
Du négatif |
–5x + 3 –6x 6x x |
>
x – 5 > –8 < 8 <
4/3 |
|
|
a > b alors? |
a + 10 a – 10 10a a / 10 –10a |
>
b + 10 >
b – 10 >
10b >
b / 10 <
–10b |
|
|
Impossible Sans solution |
2x + 10 – x x + 10 10 |
>
x + 20 >
x + 20 >
20 ??? |
|
|
Multiplication par une
variable Attention, danger Impossible si la nature de la variable n'est pas
connue. |
x ax ax |
>
5 >
5a Vrai que si a positif! <
5a Sinon |
|
Division Attention ne jamais diviser par zéro ou par une
variable dont vous ne savez pas si elle peut prendre la valeur nulle. |
(2x – 10) / 5 2x – 10 5 x |
>
x – 3 >
5x – 15 >
3x <
5/3 |
|
Carrés Deux solutions: l'une positive l'autre négative. |
x² – 25 x² x x |
>
0 >
25 >
5 <
– 5 |
|
Carrés (suite) Pas de solutions (Ou alors imaginaires) |
x² + 25 x² x |
>
0 >
– 25 >
??? |
|
Déductions On donne x > 5. Que dire de 2 x + 3? |
x 2x + 3 2x 2x + 3 2x + 3 |
>
5 ? >
2 x 5 >
10 + 3 >
13 |
|
Déductions (suite) |
x 3 – 2x –2x 3 – 2x 3 – 2x |
>
5 ? <
– 5 x 2 <
– 10 + 3 <
– 7 |
|
Parenthèses |
2(x – 20) 2x – 40 – 70 x |
>
3(4x + 10) >
12x + 30 >
10x <
– 7 |
|
Double inégalité On procède comme si l'on traitait chacune séparément |
– 2 < – 10 < – 18 < – 9 < 9 > |
(8 – 2x) / 5 8 – 2x – 2x – x x |
<
– 10 <
– 50 <
– 58 <
– 29 >
29 |
|
1.
Résolution comme les équations en
additionnant, soustrayant, multipliant ou divisant chaque membre jusqu'à
isoler la variable à calculer. 2.
Mais attention à changer le sens de
l'inégalité lorsqu'on intervertit les côtés et, aussi, lorsqu'on multiplie
par un nombre négatif. 3.
Ne jamais multiplier ou diviser par une
variable sans maîtriser parfaitement son signe. Ne jamais diviser par zéro ou
par une expression qui pourrait être nulle. |
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()