|
|||||||||||||||||||||||||||||||||
![]()
Poème d'Hervé
Bazin (1911−1996)

Voir Poésie
|
MULTIPLICATION (-) (-) = + moins
par moins égal plus Comment
expliquer ce renversement de situation ? C'est la règle des signes. Valable pour la multiplication comme pour
la division. |
3 x
4 = 12 –3
x 4
= –12 3 x (–4) = –12 –3
x (–4) =
12 |
|
J'ai déjà une
bonne idée, mais je voudrais être convaincu immédiatement et définitivement >>> |
|
Cas où ça ne marche pas selon Mots de tête incurables de Pierre Légaré
|
Une
pelure de banane sur un trottoir verglacé, ça ne s'annule pas. |
Voir Pensées & humour
|
|
||||||||||
|
|
||||||||||
|
|
||||||||||
|
|
||||||||||
|
Même
chose avec un codage |
|
|
X 1 je continue, et X (–1) je change de sens.
|
|
Cette explication est calquée sur la méthode de calcul
des baguettes chinoises:
les
pièces sont remplacées par des baguettes de deux couleurs symbolisant les gains
et les dettes.
Voir Résoudre
les tracas de calcul
|
|
|||
|
PROPRIÉTÉ
GÉNÉRALE – Distributivité de la
multiplication sur l'addition |
|||
|
|
a ( b + c) = a . b + a . c |
||
|
|
10 (2 + 3)
= 10 x 2 + 10 x 3 = 50 |
||
|
Cette propriété va nous aider à démontre que
moins par moins fait plus. Nous allons successivement remplacer c. |
|||
|
CAS PARTICULIER: c =
–b |
|||
|
|
a
( b +
c ) a
( b + (–b)
) a ( b – b) ) 0 |
= a . b + a . c = a . b + a . (–b) = a . b + a . (–b) = a . b + a . (–b) |
|
|
|
– a .
b |
= a (–b) |
|
|
CAS PARTICULIER: c =
–b & a = –d |
|||
|
|
a
( b +
c ) a
( b + (–b)) 0 |
= a .
b +
a . c = a . b + a . (–b) = (–d)
b + (–d) (–b) |
|
|
|
0 |
= –
d . b + (–d) (–b) |
|
|
|
d . b |
= (–d) (–b) |
|
|
|
|
|
MOINS par MOINS donne PLUS. |
|
|
|
||
|
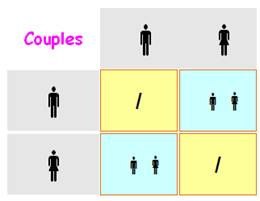
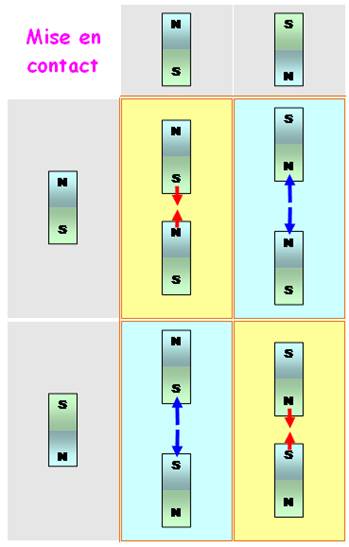
HOMMES
– FEMMES
|
AIMANTS
|
|
![]()