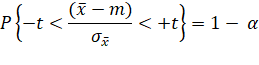|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
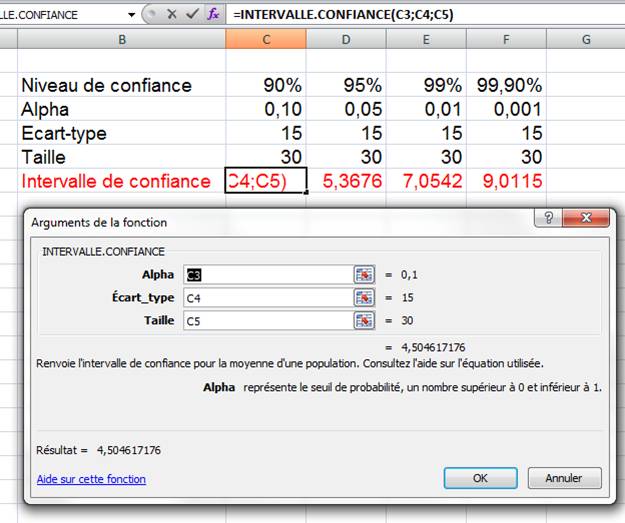
Intervalle de confiance Dans une classe, je sais
calculer la moyenne de la taille de mes
élèves. Mais comment connaître la taille
moyenne dans un département, dans la France? On procédait* par
échantillonnage en choisissant un petit nombre d'individus et en projetant la
moyenne de l'échantillon sur la population complète. Deux questions reliées:
quelle taille doit faire l'échantillon et sur quel degré de confiance je peux
compter pour toucher juste la moyenne cherchée? Nous allons procéder en
quatre temps:
* Aujourd'hui, le recensement de la population est bien entendu
nominatif. On compte tout le monde, un par un. |
Anglais: Confidence
interval
|
|
|
|
Avec un fusil,
mettre ma balle en plein dans le mille les yeux bandés? Pas possible, ou
alors je suis hyper-chanceux. Par contre, avec un tromblon qui disperse
légèrement les balles, j'ai plus de chance de toucher le mille. Sur 100 tirs
combien de fois vais-je réussir? Tout est dans la taille de l'ouverture du
tromblon …
Cette probabilité est le niveau
de confiance (C) ou le niveau de risque
(
|
|
|
|
|
|
Note: l'écart type de dit standard deviation en anglais.
|
|
|
|
|
|
En
gros
|
|
|
|
||
|
|
|
|
|
|
||
SOURCE: France 5 – Le magazine de la santé – Les publications scientifiques
sont-elles fiables? – David Zavaglia – 21/11/2013