calculs de probabilités

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/10/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	PROBABILITÉS
Débutants Dénombrement	Général			Glossaire Probabilités
INDEX Probabilités et statistiques Nombre en grand nombre	Probabilités	Grands nombres	Pile ou Face	Famille
	Principe Multip.	Moyenne & Médiane	Dés	Anniversaire
	Hasard	Coïncidences	Historique	Pari de Pascal
		Sommaire de cette page >>> Approche >>> Une énigme – Vanille ou chocolat? >>> Méthode >>> Produit >>> Choix de la méthode >>> Exclusifs >>> Non exclusifs >>> Conditionnel

Blagues classiques sur les probabilités et les statistiques

Docteur à son patient: j’ai une bonne et une mauvaise nouvelle pour vous. La mauvaise c'est que vous avez une maladie grave dont, en moyenne, seule une personne sur dix peut y survivre.

- Horreur! Mais qu'elle est la bonne ?

- Mes neuf derniers patients sont morts.

Pourquoi emmènes-tu une bombe dans l'avion? C'est simple, j'ai lu les statistiques: une chance sur 1000 qu'il y ait une bombe à bord, mais seulement une chance sur un milliard qu'il y en ait deux!...

Les statistiques en la matière sont simples: un bébé sur cinq est jaune. Tu comprends pourquoi, ma femme et moi avons décidé d'en rester à nos quatre enfants.

Voir Pensées & humour

PROBABILITÉS – CALCUL

Le calcul des probabilités est déroutant. Il n'est pas toujours intuitif. Quelques règles strictes, une bonne méthode et tout devient plus facile.

À la base: un bon dénombrement, et une appréciation des relations entre les événements possibles:

exclusifs, conditionnels…

Pour se familiariser, voir

Pour débuter, voir

Pour compter les objets, voir

Voir aussi

Jeux de hasard (amusements, loto, tiercé …)

Probabilités – Glossaire

Dénombrement

Statistique

Devinettes

Savez-vous ce qu'est une crue centennale?

Quelle est sa probabilité sur cent ans?

Trois souris se trouvent au sommet d'un triangle équilatéral. Soudain, chacune choisit son sens et s'élance sur le périmètre, toutes à la même vitesse. Quelle est la probabilité qu'elles ne rencontrent jamais ?

Solutions

APPROCHE – La clé

Ratio

du nombre de cas favorables

sur le nombre de cas total possibles

P = N favorables / N total

Si tous les cas sont favorables:

Événement certain

P = N / N =

Si tous les cas sont défavorables:

Événement impossible

P = 0 / N =

Si quelques cas sont favorables

P = N favorables / N

0 < P < 1

Exemples

0, 5 =

1/2

Probabilité d'obtenir pile en lançant une pièce.

Un cas favorable pour 2 cas possibles.

0, 166 =

1/6

Probabilité d'obtenir un six en lançant un dé.

Un cas favorable pour 6 cas possibles.

0, 833 =

5/6

Probabilité de ne pas obtenir un six en lançant un dé.

Cinq cas "favorables" pour 6 cas possibles.

= 1 – 1/6

C'est aussi la probabilité d'avoir l'un des chiffres:
ce qui est tout le temps vrai: P = 1,

tout en retirant l'arrivée du 6, non désiré: P = 1/6.

Règle

P(E) = 1 – P(non E)

La probabilité d'un événement et la probabilité qu'il ne se produise pas donne "l'évènement sûr" (probabilité = 1).

Une énigme classique – Vanille ou chocolat?

Trois paniers contenant

2 barres au chocolat

1 barre chocolat et une barre vanille, et

2 barres à la vanille.

Après avoir retiré une barre au chocolat, quelle est la probabilité que la seconde soit aussi au chocolat?

Une réponse un peu rapide serait 1/2. Mais un bon calcul de probabilité va montrer qu'il s'agit de 2/3.

Nommons les barres:

C1 C2 / C3 V1 / V2 V3

Au premier tirage: 3 possibilités (C1 ou C2 ou C3).

Quels sont les voisins dans le panier?

C1 avec C2

C2 avec C1 et

C3 avec V1

Soit deux cas où c'est le chocolat; deux cas favorables.

Voir Énigmes filles ou garçons

Historique

Les deux problèmes qui suivent ont été posés par le Chevalier de Méré au milieu XVIIe siècle. Son interrogation: qu'est-ce qui est le plus probable?

Probabilité d'un 6 en 4 jets d'un dé; ou

Probabilité d'un double-6 en 24 jets de deux dés.

Chacune étant proche de 50%.

C'est Pascal qui calcula les bonnes réponses, marquant le début des calculs de probabilités:

Voir Partage de Méré-Pascal / Probabilités avec les dés

MÉTHODE
Probabilité d'obtenir au moins un six en 4 lancers de un dé:		0, 518 = 1 – (5 / 6)⁴
Calcul	Cette probabilité peut se calculer en prenant la probabilité d'obtenir un "6", ajoutée à celle d'obtenir deux "6", etc. Mais, il y a plus simple en prenant le problème à l'envers:
Calculer la probabilité de ne pas obtenir de "6" du tout.		P(non6)
Et, en déduire la probabilité d'obtenir un ou plusieurs "6" qui sera son complément à 1.		P(6) = 1 – P(non6)
Or, pour chaque lancer:		P(non6) = 5/6
Les résultats de chaque lancer sont indépendants les uns des autres, alors, la probabilité résultante est le produit des probabilités élémentaires:		P(non6) = (5/6)⁴ = 0, 482
Et, finalement:		P(6) = 1 – P(non6) = 0,518
*Attention: On remarque que la probabilité ne se laisse pas faire avec simplicité. Ici,* chaque lancer ayant une probabilité de 1/6, la probabilité résultante n'est pas: 4 fois 1/6 = 2/3 = 0, 666 Avec plus de lancers, on dépasserait une probabilité maximale de 1! >>>

PRODUIT
Probabilité d'obtenir un double six en 24 lancers de deux dés; et en 25: C'est la bascule autour de 50%.		0, 491 = 1 – (35 / 36)²⁴ 0, 505 = 1 – (35 / 36)²⁵
Calcul	Cette probabilité peut se calculer en prenant la probabilité d'obtenir un "double 6", ajoutée à celle d'obtenir deux "double 6", etc. Mais, il y a plus simple en prenant le problème à l'envers:
Calculer la probabilité de ne pas obtenir de "double 6" du tout.		P(nonD6)
Et, on en déduit la probabilité d'obtenir un ou plusieurs "double 6" qui sera son complément à 1.		P(D6) = 1 – P(nonD6)
Or, pour chaque lancer:		P(nonD6) = 35/36
Les résultats de chaque lancer sont indépendants les uns des autres, alors, la probabilité résultante est le produit des probabilités élémentaires.		P(nonD6) = (35/36)²⁴ = 0,509
Et, finalement:		P(D6) = 1 – P(nonD6) = 0,491
*Attention:* On remarque que la probabilité ne se laisse pas faire avec simplicité. *Ici,* chaque lancer ayant une probabilité de 1/36, la probabilité résultante n'est pas: 24 fois 1/36 = 2/3 = 0, 666 >>>

Propriété

P(E et F) = P(E) x P(F)

(E & F indépendants)

La probabilité que deux événements se produisent est égale au produit de la probabilité

de chaque événement, à la condition que ces événements soient totalement indépendants. Comme les jets de dés par exemple.

Explications complémentaires – Choix de la méthode

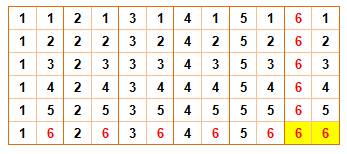
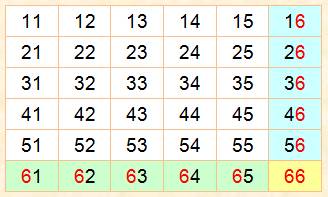
Comment dénombrer?

Avec deux dés: 36 possibilités de sorties (on dit: issues). Par exemple: (1,1) ou (1,2) ou … (6,5) ou (6,6). Mais un seul cas de double-six. La probabilité du double 6 est 1/36.

Autre raisonnement: la probabilité d'un 6 pour chaque dé est 1/6. Pour deux dés, les deux jets étant indépendants, la probabilité est le produit des probabilités soit 1/6 x 1/6 = 1/36.

Les 36 issues d'un jet de deux dés

Une seule possibilité sur 36 pour le double-six.

Pourquoi 1/(6)² et pas 1 – (5/6)²?

Le graphe des situations donne la réponse.

En lignes vertes

Le chemin du double "succès" est direct.

En lignes bleues

La probabilité 5/6 d'un "échec" sur un dé se retrouve sur deux chemins différents.

NB l'emploi de la multiplication (en descendant) et de l'addition (en bilan des possibilités).

Pourquoi 1 – (35/36)²⁴
et pas (1/36)²⁴

Là aussi, il faut choisir le chemin du "succès", en ligne directe (verte). C'est le cas pour du non-double six

Par contre, il existe de multiples façons d'arriver au double six (rouge). Le calcul serait bien compliqué.

EXCLUSIFS
Probabilité d'obtenir la somme 3 ou la somme 4 en lançant 2 dés:				0, 1388... = 5 / 36
Calcul	Avec deux dès, il ya 36 possibilités.
S = 3		si ou si	2 et 1 1 et 2		P(S=3) = 2/36
S = 4		si ou si ou si	3 et 1 1 et 3 2 et 2		P(S=4) = 3/36
Bilan		5 possibilités	P(S=3 ou S=4) = 2/36 + 3/36 = 5/36

Propriété

P(E ou F) = P(E) + P(F)

si E et F sont exclusifs

La probabilité de l'un ou l'autre des événements est la somme de leur probabilité respective, si les événements ne sont pas simultanés. On dit "exclusifs".

NON EXCLUSIFS
Probabilité de tirer un "6" en jetant 2 dés:		0, 3055... = 11 / 36
Calcul	Toujours 36 possibilités
La probabilité de tirer un "6" avec le premier dé est de			6/36
Avec le deuxième dé, elle est aussi de			6/36
La somme donne 6/36 + 6/36 =			12/36
Oui mais, comptons bien: dans le lot il y a un "double 6"; il ne compte pas pour 2, mais seulement pour 1			1/36
A notre somme, il faut retrancher la probabilité des deux événements simultanés: 12/36 - 1/36 =			11/36
*Illustration* 6 cas favorables avec le premier dé + 6 cas favorables avec l'autre dé – un cas compté en double.

Propriété

P(E ou F) = P(E) + P(F) - P(E et F)

si E et F ne sont pas exclusifs

Comme pour les événements exclusifs, la probabilité d'un événement ou d'un autre est additive,

mais en prenant la précaution d'éliminer ceux qui sont en double, car non exclusifs.

Voir Combinatoire pour une formule analogue

CONDITIONNEL

Probabilité de tirer un "double 6", sachant que le premier dé lancer a déjà donné un "6":

1 / 36 = 0, 0277… = 2,77%

Notation

On dit que la probabilité de l'événement E
est conditionnée à celle de l'événement F.
On note: P(E/F).

On lit: "probabilité de E si F".

Propriétés

P(E / E ) = 1

Lorsque E se produit, l'événement est certain.

P(E / F ) = 0

si E et F sont exclusifs

Lorsque F s'est produit,

E ne se produira pas.

P(E / F ) = P(E)

si les événements sont indépendants

Si E ne dépend pas de F, sa probabilité conditionnée à F

est tout simplement celle de E tout seul.

Généralisation

P(E et F) = P(E/F) x P(F)

et aussi

P(E et F) = P(F/E) x P(E)

Comme pour les événements indépendants la probabilité que deux événements liés se produisent est bien un produit de deux probabilités.

Exemples	Probabilité que le premier dé soit un 6 et que le deuxième dé soit un 6:		?
	Probabilité que le deuxième dé soit un 6, *sachant* que le premier est un 6:	1 / 6
	Probabilité d'obtenir un 6 avec le premier dé:	x 1 / 6
	Soit, la probabilité cherchée:		= 1 / 36

Voir Fille ou garçon

Exemple de calcul – CYCLE DE VIE

Soit 10 personnes.

Chaque année, une meurt et une vient au monde.

Au bout de 10 ans,

la probabilité que l'une d'elles soit vivante est de 1/3.

En effet:

au bout d'un an, la probabilité est 9/10.

Pour 10 ans, elle est (9/10)¹⁰= 0,34868.

Devinettes – Solutions

Les trois souris: chacune choisit un sens de parcours parmi 2.

Soit 8 possibilités pour les trois souris (2x2x2 = 2³).

Elles ne se rencontrent jamais si elles tournent toutes dans le même sens.

Soit 2 possibilités.

La probabilité de non-rencontre est: 2/8 = ¼ = 25%.

Savez-vous ce qu'est une crue centennale?

Quelle est sa probabilité sur cent ans?

Crue centennale

Curieusement, une crue centennale ne se produit pas tous les cents ans. En fait, elle a une probabilité de se produire de 1/100 sur l'année.

La probabilité de non-occurrence sur un siècle est égale à: (99/100)¹⁰⁰ = 0,366032… et la probabilité d'occurrence est égale à : 0,633967…

Crue n-ennale

Une crue n-ennale a une probabilité de 1/n de se produire dans l'année. La probabilité d'occurrence en n années est égale à

Principaux types de crues

Voir Crue – Wikipédia

Retour / Géographie – Index

Suite	Introduction aux probabilités avec les dés Loi de Poisson Moyenne & Médiane Pari de Pascal
Voir	Arbre pondéré Chances aux tirage Chapeaux et e Coïncidences Courbes élémentaires Définition du domaine Définitions et symboles Dénombrement – Index Factorielles Hasard Jeux de hasard (loto, tiercé …) Jeux, énigmes et puzzles Laplace Logique Nombres et magie Pensées et Humour – Index Probabilités – Glossaire Probabilités et logique Quantité de 3 Statistiques – Index Tirage sur 10 milliards Trois dés et une urne Trois pièces Types de moyennes
Sites	Probabilités et Statistique de Jean-Michel JOLION ( INSA )
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Probabil/ProbCalc.htm