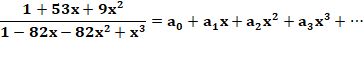NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/03/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	NOMBRES
Débutants Général	Partition en CUBES			Glossaire Général
INDEX Nombres en puissance Puissance	S'y retrouver	Partition cubes	Taxicab
		Sommaire de cette page >>> Les nombres taxicab connus >>> Histoire ou légende ? >>> Autour des taxicab >>> Presque Fermat (à 1 près) >>> Roman indien

Nombres TAXICAB

Somme multiples de cubes

Pourquoi taxicab? Une anecdote (ou une légende) entre Hardy et Ramanujan. Une sorte de jeu entre mathématiciens habitués à jongler avec les nombres.

Quels sont les plus petits nombres qui sont n fois somme de cubes?

Les nombres taxicab connus

Nombres taxicab d'ordre n

Ta(n) = le plus petit nombre qui est somme de n fois deux cubes.

Ta(6)

24 153 319 581 254 312 065 344

= 582162^3 + 28906206^3 = 3064173^3 + 28894803^3 = 8519281^3 + 28657487^3 = 16218068^3 + 27093208^3 = 17492496^3 + 26590452^3 = 18289922^3 + 26224366^3

Ta(7) n'est pas encore connu.

Somme de nombre relatifs: exemples

91 = 4³ + 3³ = 6³ – 5³

189 = 4³ + 5³ = 6³ – 3³

HISTOIRE ou LÉGENDE ?
Le mathématicien anglais G.H. Hardy visitait le fameux mathématicien indien Srinivasa Ramanujan à l'hôpital. Mon taxi avait vraiment un numéro quelconque: "1 729", dit le premier. Mais, pas du tout, répondit Ramanujan, c'est le plus petit nombre exprimable par la somme de deux cubes de deux manières différentes ".	Depuis, de tels nombres sont généralisés et baptisés Taxicab. Bernard Frénicle de Bessy (1605-1675) qui connaissant cette propriété. Est-ce que Ramanujan en avait connaissance?
English The famous anecdote is that during one visit to Ramanujan in the hospital at Putney, Hardy mentioned that the number of the taxi cab that had brought him was 1729, which, as numbers go, Hardy thought was "rather a dull one". At this, Ramanujan perked up, and said "No, it is a very interesting number; it is the smallest number expressible as a sum of two cubes in two different ways."
Quitte à nuire un peu à la légende qui veut que Ramanujan ait calculé instantanément de tête l'étonnante propriété de 1729, De Konninck dans son dictionnaire indique que la remarque concernant 1729 avait déjà été formulée dès 1657 par Bernard Frénicle de Bessy, et qu'il est possible que Ramanujan n'ait fait que se souvenir d'une lecture. Cité par Jean-Paul Delahaye – Mille Collections de Nombres

Autour des Taxicab

Quelques doubles sommes de cubes

Frenicle 1729

1^3+ 12^3 =	9^3 + 10^3 =	1 729
2^3+ 16^3 =	9^3 + 15^3 =	4 104
2^3+ 34^3 =	15^3 + 33^3 =	39 312
10^3+ 27^3 =	19^3 + 24^3 =	20 683

Autres

2^3 + 24^3 =

18^3+ 20^3 =

13 832

Avec des nombre négatifs 91 devient le plus petit:

91 = 6³ + (–5)³ = 4³ + 3³

Suite Somme de cubes deux fois

Puissance 4?

Hardy a demandé quel est le nombre le plus petit somme deux fois de deux nombres à la puissance quatrième.

Ramanujan répond qu'il devait être très grand, car il ne le connaissait pas.

635 378 657

= 59⁴ + 158⁴

= 133⁴ + 134⁴

Nombre découvert par Euler en 1772

Presque Fermat (à 1 près)
Presque Fermat X^n + Y^n = Z^n 9^3 + 10^3 = 12^3 + 1 Manqué d'une unité ! Voir Fermat-Wiles Combinaison 6^3 + 8^3 = 9^3 – 1 9^3 + 10^3 = 12^3 – 1 Somme 6^3 + 8^3 + 10^3 = 12^3 216 + 512 + 1000 = 1728 Division des nombres par 2 3^3 + 4^3 + 5^3 = 6^3 27 + 64 + 125 = 216 Voir Pépites	Ramanujan trouva d'autres nombres à 1 près 1^3 + 2^3 = 2^3 + 1 = 9 (trivial) 6^3 + 8^3 + = 9^3 – 1 = 728 135^3 + 138^3 = 172^3 – 1 = 5 088 447 791^3 + 812^3 = 1 010^3 – 1 = 1 030 300 999 11 161^3 + 11 468^3 = 14 258^3 + 1 = 2 898 516 861 513 65 601^3 + 67 402^3 – 83 802^3 + 1 = 588 522 607 645 609 Ces trouvailles découlent d'identités "stupéfiantes" Si: Alors Suite en Sequences Related to the Work of Srinivasa Ramanujan

Roman indien

Je me rappelle encore le problème qui lui donnait du fil à retordre. Des années auparavant, moi aussi, à l'école, j'avais eu à résoudre la même équation:

x³ + y³ = l³ + m³ = 1 729

(…) Le plus petit nombre que l'on peut poser comme la somme de deux cubes, de deux manières différentes.

x= 1; y = 12; l = 9 et m = 10.

Le premier à avoir résolu ce problème fut Ramanujan, un mathématicien d'Inde du sud. C'était un génie qui trouva la solution à l'âge de vingt-neuf ans sur son lit de mort.

Page 183 du roman Chef de Jaspreet Singh – Pocket – 2011

Suite	Nombres de Carol et nombres de Kynea – Développements et tables Nombres selon leur type Nombres = somme multiples de puissances (Orientation parmi toutes les formes de sommes de puissances)
Voir	Nombre et leurs puissances (parité, divisibilité par 6) Nombre premiers
DicoNombre	Nombre 728 Nombre 1 728 Nombre 1 729
Livre	Les nombres taxicabs – Pour la Science – Avril 2008 – Christian Boyer
Sites	OEIS A051028 – Ramanujan's a-series: expansion of (1+53x+9x^2)/(1-82x-82x^2+x^3). Et suite en: A51029 et A51030
Cette page	http://villemin.gerard.free.fr/aNombre/PUISSANC/Taxicab.htm