|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PARTITION
des NOMBRES en
SOMME de PUISSANCES C |
Génér
Voir Table des puissances des nombres
|
|
|||||
|
19 P4 |
|
La démonstration existante donne 35 termes.
79
= 4 x 24 + 15 x 14 159, 239,
319 et 399 |
|||
|
17 et 18 |
Liste finie |
Les plus petits: 63 pour 18 et 47 pour 17 |
|||
|
16 P4 |
Davenport 1939 |
Le plus petit: 31 Liste en Mathworld |
|||
|
5 P4 |
|
54
= 625 = 24 + 24
+ 34 + 44 + 44 154 = 50 625 = 44 + 64
+ 84 + 94 + 144 Les sept
configurations jusqu'à 20
|
|||
|
4 P4 |
Les deux plus
petites solutions => |
3534 = 304 + 1204 + 2724
+ 3154 6514 = 2404 + 3404
+ 4304 + 5994 |
|||
|
3 P4 |
|
6 578 = 14 + 24 + 94
= 34 + 74 + 84 |
|||
|
2 P4 |
|
17 = 14 + 24 |
|||
Voir Puissance 4
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
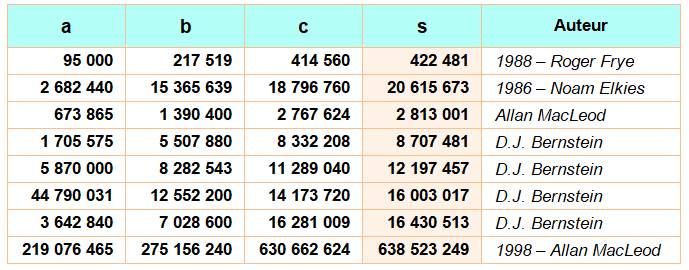
Il existe une infinité de solutions. Mais la deuxième comporte déjà des nombres
de 70 chiffres. |
s4
= a4 + b4 + c4 La plus petite configuration: 95 8004 = 84 229 075 969
600 000 000 217
5194 = 2 238 663 363 846 304 960 321 414
5604 = 29 535 857 400 192
040 960 000 422
4814 = 31 858 749 840 007
945 920 321 La première, trouvée par Noam Elkies en 1986, lequel a prouvé qu'il en existe une infinité. 2 682 4404 =
51 774 995 082 902 409 832 960 000 15
365 6394 = 55 744 561 387 133 523 724 209 779 041 18
796 7604 = 124 833 740 909
952 854 954 805 760 000 20
615 6734 = 180 630 077 292
169 281 088 848 499 041 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
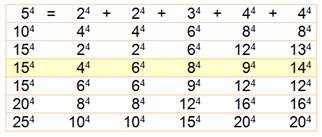
Quelques exemples de: s4 = a4 + b4 + c4
Quelques exemples de: s4 = a4 + b4
+ c4 + d4 + e4
Notez que 10, 15, 20 et 25 sont multiples de 5 et
partagent avec 5 le même type de somme Voir Bicarré,
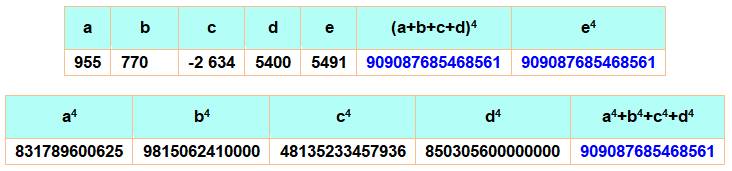
somme de bicarrés – Table / DicoNombre 15 Cas singulier avec cinq bicarrés: (a + b + c + d)4 = a4
+ b4 + c4 + d4 = e4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On peut écrire: x4 + y4 = z4 de
la manière suivante: soit: s4 + t4 = 1 |
Alors que la courbe s4
+ t4 = 1 ne passe jamais par une paire de coordonnées rationnelles
(Fermat), la
courbe s4 + t4 + u4 = 1 passe par
une infinité de points dont les coordonnées sont rationnelles (infirme la conjecture d'Euler). |
|||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Autres
identités en puissance 4 / Théorème de Waring
/ Courbes elliptiques
|
|
|||||
|
Distincts |
|
|
|||
|
2 fois 2P4 |
La plus petite
solution trouvée par Euler
en 1772. |
635
318 657 = 594 + 1584
= 1334 +
1344 3 262 811 042 = 74 + 2394 = 1574 +
2274 |
|||
|
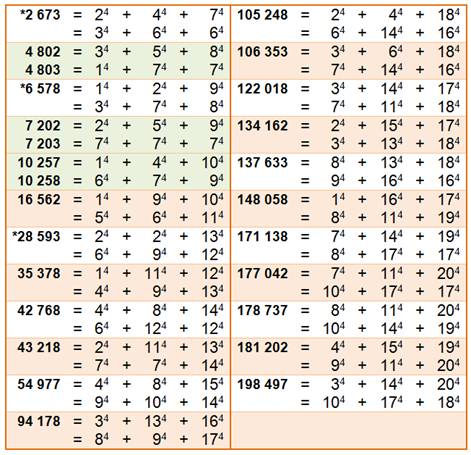
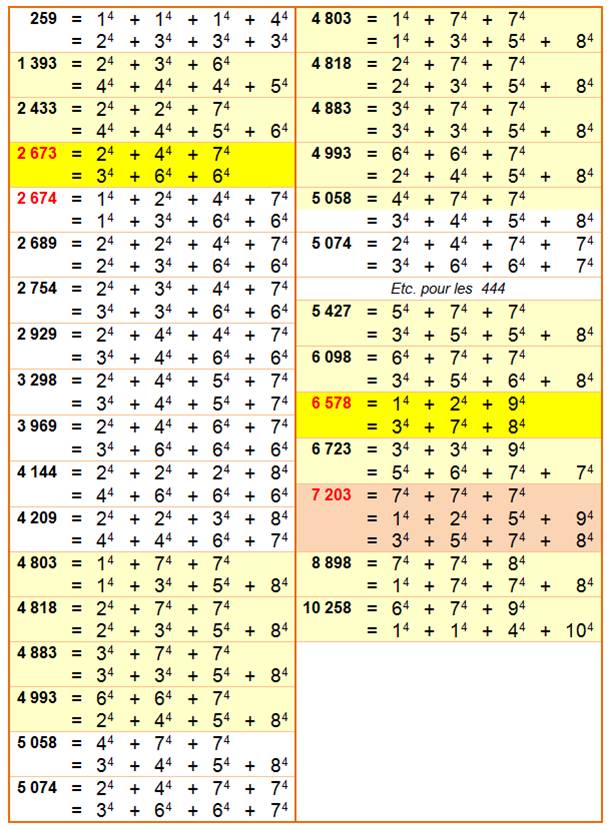
2 fois 3P4 |
Toutes
les configurations jusqu'à 20. Avec
* celles trouvées par Ramanujan comme 2 673. En
vert, les trois premières configurations à 1 près. |
|
|||
|
2 ou 3 fois 3P4 et
4P4 |
En
jaune foncé, le rappel des configurions 433
(4 pour la puissance, 3 pour la quantité de termes d'un côté de l'égalité et
3 pour l'autre côté). En
jaune clair les 434 et en blanc les 444. Toutes
les configurations (sauf pour les 444) jusqu'à une somme de 10 000. Notez
le nombre 7 203
en trois présentations.
|
||||
Voir Ramanujan-Hardy
|
|
||||
|
Général |
|
|
||
|
Somme de puissance 5
donnant une puissance 5 |
SIX puissances 5 248
832 est
la plus petite puissance cinquième égale à la somme de 6 puissances 5. CINQ puissances 5 725 est la plus petite
puissance cinquième égale à la somme de 5 puissances 5e. QUATRE puissances 5 Premier
contre exemple à la conjecture
d'Euler. Trouvé
par L.J. Lander & T.R. Parkin en 1966. Voir Nombre
144 |
248
832 = 125 =
45 + 55 + 65 + 75 + 95
+ 115 1
934 917 632 = 725 =
195 + 435 + 465 + 475 + 675 1445 = 275 + 845 + 1105
+ 1335 61 917 364 224 = 14 348 907 + 4 182 119 424
+ 16 105 100 000 + 41 615 795 893 |
||
|
Somme de puissances
de 5 distinctes |
Ce nombre est le plus grand nombre qui ne
peut pas s'exprimer comme somme de puissances cinquièmes distinctes. |
67 898 771 |
||
|
Puissance 5
particulières |
Ce
nombre est égal à la puissance cinquième de ses chiffres. |
54 748 = 55 + 45
+ 75 + 45 + 85 |
||
|
Somme de 3
puissances de 2 manières, plus coquetterie |
Avec
aussi égalité de la somme des entiers:
119 = 3
+ 54 +
62 = 24
+ 28 + 67 1 375 298 099 = 35
+ 545 + 625 = 245 + 285 + 675 231 = 39
+ 92 + 100 = 49
+ 75 + 107 16 681 039 431 = 395
+ 925 + 1005 = 495 + 755 + 1075 |
|||
|
|
||||
|
Général |
|
|
||
|
6 fois P6 |
On
ne connaît pas de somme de six puissances 6 donnant une puissance 6; ni
moins. |
|
||
|
Somme de 3 puissances
6 |
Solution
minimale d'une somme de puissances 6 égale à une autre somme de puissances 6. |
36
+ 196 + 226 =
106 + 156 + 236 =
160 426 514 256
+ 626 + 1386 =
826 + 926 + 1356 =
6 963 806 813 393 |
||
|
|
||||
|
Général |
|
Note: 137 a été corrigé
en 143 selon la source Mathworld |
||
|
Somme de 3 à 6
puissances 7 |
Aucune solution |
|
||
|
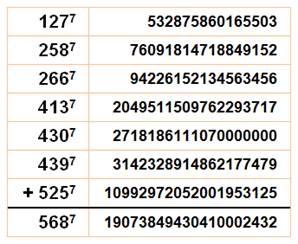
Somme de 7
puissances 7 |
568
est
la plus petite puissance septième décomposable en somme de seulement 7 autres
puissances septièmes. |
|
||
|
Somme de 8
puissances 7 |
102
est
la plus petite puissance septième décomposable en somme de seulement 8 autres
puissances septièmes. |
1027 = 127 + 357 + 537 + 587 + 647 + 837 + 857 + 907 |
||
|
Somme de 9
puissances 7 |
62
est
la plus petite puissance septième décomposable en somme de seulement 9 autres
puissances septièmes. |
627 = 67 + 147 + 207 + 227 + 277 + 337 + 417 + 507 + 597 |
||
|
|
||||
|
Général |
|
Note: 273 a été corrigé
en 279 selon la source Mathworld 4
863 est
le plus petit. Mais,
tout entier suffisamment grand peut s'écrire sous la forme d'une somme de 163
puissances huitièmes. |
||
|
Somme de 8
puissances 8 |
14098 = 908 + 2238
+ 4788 + 5248 + 7488 + 10888 +
11908 + 13248 |
|||
|
Sommes de puissances 8 |
765 381 793 634 649 192 581 218 = 818 + 5398 + 9668 =
1588 + 3108 + 4818 + 7258 + 9548 Scott Chase cité par Jean-Charles Meyrignac |
|||
|
Notation des sommes
de puissances |
On
note les sommes de puissances en donnant
trois nombres
On
réserve la notation à la valeur minimum de la somme L'égalité
suivante est notée (8, 1, 9): 1
1678 = 1908 +
2718 + 2848 + 3488 + 3668+ 5588
+ 5608+ 10408 + 10948
= 3 440 066 582 016 500 042 119 041 Nuutti Kuosa - 2000 |
Voir généralisation:
Théorème de Waring
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Beaucoup d'autres
configurations en: From MathWorld – A Wolfram Web Resource.
|
|
Sites |
|
|
Cette page |
![]()