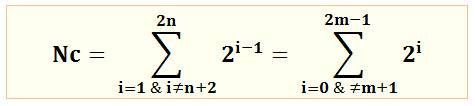|
||||||||||||||||||||||||||
![]()
|
F |
Nombre / Diviseurs / Multiplicatif / Premiers |
|
Définition |
NOMBRES de CAROL Nombre
de la forme:
n est un entier strictement positif Voir Puissances de 2 Si
ce nombre est premier,
c'est un nombre premier de Carol. Le
nombre 2n – 1 est un nombre de
Mersenne. NOMBRES de KYNEA Nombre
de la forme:
n est un entier strictement positif Si
ce nombre est premier, c'est un nombre premier de
Kynea. |
|
Exemples |
n
= 3 => (23 – 1)2 – 2 = (8 – 1)2 – 2 = 47 et
47 est premier; c'est un nombre premier de Carol. n
= 3 => (23 + 1)2 – 2 = (8 + 1)2 – 2 = 79 et
79 est premier; c'est un nombre premier de Kynea. |
|
Famille |
|
|
Commentaire |
|
|
|
||
|
Propriétés numération binaire |
Exemple
Nc = 1n – 2 0 1n
+ 1 Exemple: Nc(4) =
1510 = 11 0 11111 Voir Table |
|
|
Propriété de divisibilité |
|
|
|
Anglais |
|
|
|
|
||
|
Propriétés numération binaire |
Nk = 1 0n-1 1n + 1 Exemple: Nc(4) =
28710 = 100011111 Voir Table |
|
|
Propriété de divisibilité |
|
|
|
Anglais |
|
|
|
|
|
|
Indice
des nombres premiers de Carol 2, 3, 4, 6, 7, 10, 12, 15, 18, 19, 21, 25, 27, 55,
129, 132, 159, 171, 175, 315, 324, 358, 393, 435, 786, 1 459, 1 707, 2 923, 6
462 … Il en existe seulement 25 pour atteindre la
valeur 41000. Le plus grand premier de Carol, trouvé en 2007
par Cletus Emmanuel, a pour indice: 253 987 et c'est
le numéro 40. Voir ce nombre sur le
site The Largest Known
Primes |
|
|
|
|
|
Le plus grand premier de Kynea,
trouvé en 2005 par Cletus Emmanuel, a pour indice: 281
621 et c'est le numéro 46. Voir ce nombre sur le
site The Largest Known
Primes Nombres
composés de Kynea non multiple de 7
|
|
Voir Binaire
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/PremCaro.htm
|
![]()