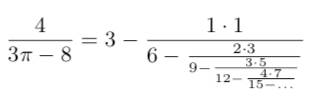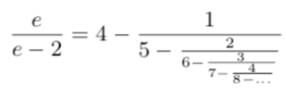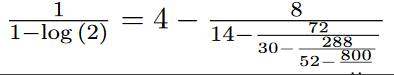|
||||||||||||||||||||
![]()
|
L'homme
qui connaissait l'infini. Un
génie du XXe siècle. Un artiste des équations. "An equation for me has no
meaning, unless it express a thought of
God". |
|

|
|
|||||||||||||||||||||
|
|||||||||||||||||||||
Une
des identités numériques de Ramanujan

|
1887 |
|
Ramanujan et les preuves.
|
|
|
1903 |
16 ans |
|
|
|
1904 |
17 ans |
|
|
|
1906 |
19 |
|
|
|
1909 |
22 |
|
|
|
1910 |
23 |
Le décollage
|
|
|
1911 |
24 |
|
|
|
1912 |
25 |
|
|
1913 |
26 |
Prodige
|
|
|
1914 |
27 |
|
|
|
|
|
|
|
|
1919 |
32 |
|
|
|
1920 |
33 |
|
|
Bernard Frénicle de Bessy (1605-1675) qui connaissant cette
propriété. Est-ce que Ramanujan en avait connaissance? |
English The famous
anecdote is that during one visit to Ramanujan in the hospital at Putney,
Hardy mentioned that the number of the taxi cab that had brought him was
1729, which, as numbers go, Hardy thought was "rather a dull
one". At this,
Ramanujan perked up, and said "No, it is a very interesting number; it
is the smallest number expressible as a sum of two cubes in two different
ways." |
Voir Développements sur les nombres TAXICAB
|
|
|
|
Quelques
jalons
|
|
|
Première lettre de Ramanujan à Hardy: j'ai découvert
une fonction qui représente exactement le nombre des nombres premiers
inférieur à x. Page 29 Voici donc l'hypothèse
de Riemann: vous prenez la fonction zêta et vous y introduisez des nombres
complexes (…) Selon cette hypothèse, à chacun des points où la fonction est
égale à la valeur zéro, la partie réelle aura une valeur de 1/2. Page 66 Imaginez un barbier
qui tous les jours rase les hommes de sa ville qui ne se rasent pas tout
seuls. Le barbier se rase-t-il? Page 74 Aucun nombre jusqu'à 24 n'a plus
de six diviseurs. 22 en a quatre, 21 en a six. Mais 24 en a huit. 24 est
divisible par 1, 2, 3, 4, 6, 8, 12 ou 24. Donc, je définis un nombre hautement composé comme un nombre
qui comporte plus de diviseurs que tous les nombres venant avant lui. Page 219 À présent, Hardy a établi de manière irréfutable qu'il
existe une infinité de zéros
le long de la ligne critique … Page 227 Puis nous posons un nombre Q, qui sera plus grand que
tous les nombres premiers multipliés par entre eux. Autrement dit: Q = 2 x 3
x 5 x 7 x 11 x 13 x … x P + 1… Démonstration
d'Euclide Page 262 C'est pourquoi 31,
331, 3 331, 33 331, 333 331, 3 333 331 sont des
nombres premiers, mais pas 33 333 331. Page 278 Des lakhs de gens venus de chez nous se
joignent aux forces militaire (…) La guerre
en cours affecte des crores d'individus, des millions. Note: lakh = 100 000 et crore =
10 000 000. Page 327 Il aime presque tous les nombres premiers. Il aime 32 671,
pour des raisons qui lui échappent (…) Il aime aussi les nombres
hautement composés, ce sont le 4 et le 36 qu'il aime le plus (…) Page 330 Comptant tous les nombres de 1 à 1 000 000, puis les
rangeant par degré de rondeur. "1 000 000, Hardy c'est très rond,
m'a-t-il ainsi dit un jour. Il comporte douze facteurs premiers, tandis que
si vous prenez tous les nombres entre 999 991 et 1 000 010,
la moyenne n'est que de 4. Page 339 Ramanujan extrait de sa poche une
coupure de presse et la tend à Hardy. "Énigmes
dans une auberge de village" (…) L'autre jour, racontait William Rogers
aux autres villageois (…) un endroit
qui s'appelle Louvain (…) la maison de son ami se trouvait dans une longue
rue … Voir l'énoncé de l'énigme
et sa solution Page 359 |
Ce qu'en disait Hardy
|
Il travaillait par induction
à partir d'exemples numériques, beaucoup plus que ne le faisait la majorité
des mathématiciens contemporains …; mais, en alliant sa mémoire, sa patience
et sa puissance de calcul, il aboutissait à une capacité de généralisation,
une appréciation des formes, et une flexibilité pour de rapides modifications
de ses hypothèses, qui étaient souvent surprenantes et le rendait sans rival
à ce jour dans son domaine de compétence. |
|
Formules improbables à la manière de
Ramanujan
|
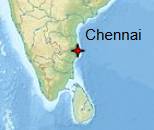
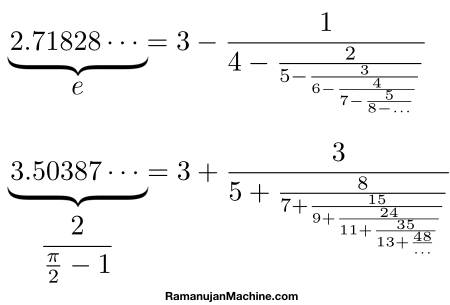
Les ingénieurs de l’institut de Technion (Israël)
ont développé une machine informatique à base d'IA – The Ramanujan machine – capable de proposer
de nouvelles formules impliquant des constantes et des fractions
continues. À charge aux mathématiciens de les prouver. Exemples
|
Voir le site: The Ramanujan Machine / Accès aux nouvelles formules
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Livres |
|
|
Sites |
|
|
Cette
page |
![]()