|
||||||||||||||||||||||||||||||||||
![]()
|
Théorème des TROIS PERPENDICULAIRES La propriété. Sa démonstration (simple) basée sur les cas
d'égalité des triangles. Ses conséquences. |
Voir Perpendiculaire – orthogonal
et normal
|
|
||
|
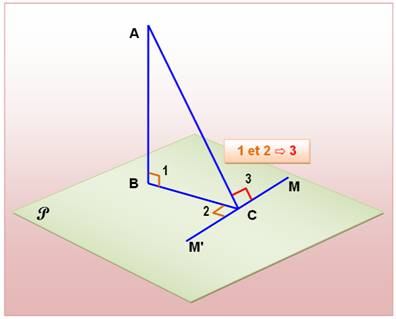
Énoncé du théorème Si une droite (AB) est perpendiculaire à un plan (P) et que, par son
pied (B), on mène la perpendiculaire (BC) à une
droite quelconque du plan (MM'), la droite (AC) qui joint le pied (C) de
cette seconde perpendiculaire à un point quelconque de la première(A), est
perpendiculaire à la droite du plan (MM'). |
|
|
|
|
||
|
|
||
|
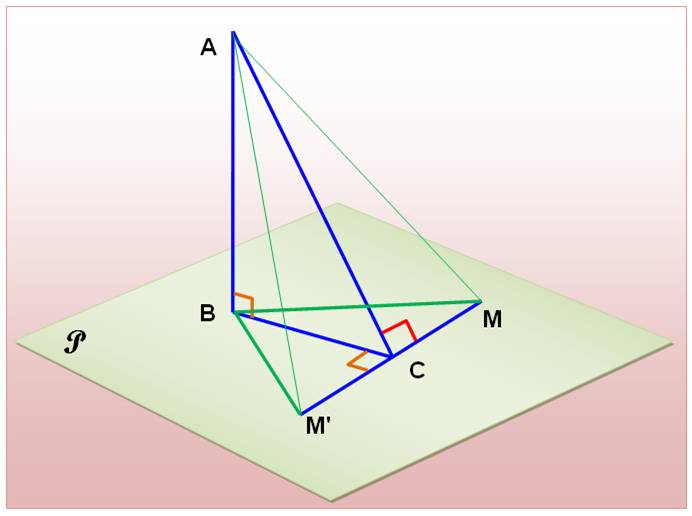
Hypothèses BC et MM' appartiennent au plan P. Prouver que: Construction Lignes vertes avec: |
AB MM' AC CM = CM' |
|
|
Démonstration
Ces deux triangles sont égaux. Dans ces triangles
Ces deux triangles sont égaux. Dans ces triangles
|
BM = BM' BM = BM' AB est commun
AM = AM' AM = AM' AC est
commun CM = CM'
|
|
|
|
||
|
Théorème Si deux droites (D et D') sont parallèles, alors que D est
perpendiculaire au plan P, alors D' l'est aussi La démonstration reprend les éléments de la démonstration précédente
et se poursuit comme suit: |
|
|
|
Nous savons (construction)
que: Conclusion: MC est perpendiculaire
au plan qui contient ces segments.
MC est perpendiculaire à
toute droite du plan en particulier D'.
|
MC MC MC D et D' D' ABC = ECB
= D' D'
|
|
![]()
|
Retour |
|
|
Aussi |
|
|
Cette page |
![]()