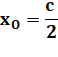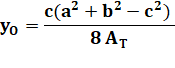Orientation Glossaire	Atlas / Géométrie / Figures / Droites Médiane / Hauteur / Bissectrice
Débutant DicoMot DicoNombre	MÉDIATRICE
	Sommaire de cette page >>> Définition et propriétés >>> Anglais >>> Construction >>> Amusement: médiatrice et complexes >>> Étude sur les médiatrices >>> Coordonnées du centre du cercle circonscrit

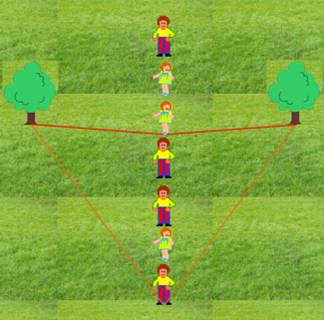
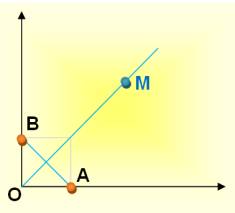
Approche	Les enfants, vous voyez les deux arbres? Chacun va se mettre à un endroit tel qu'il sera à une égale distance des deux arbres. Ouais! Vous formez une médiatrice!
Définition	Médiatrice d'un segment: ensemble des points équidistants aux extrémités du segment; ces points se trouvent sur la perpendiculaire au segment en son milieu. Aussi: La médiatrice du segment [AB] est la droite perpendiculaire à (AB) qui passe en son milieu. Médiatrices du triangle: les trois droites perpendiculaires à chaque côté du triangle en leur milieu.
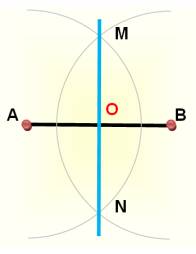
Construction	Pour tracer la médiatrice du segment AB: Prendre un compas et garder son ouverture (R) pour tracer un cercle de centre A et un autre de centre B. Ils se coupent en deux points M et N. Chacun est à une distance R de A et de B: MA = MB = NA = NB La droite qui passe par M et N est la médiatrice du segment AB

Voir Constructions élémentaires

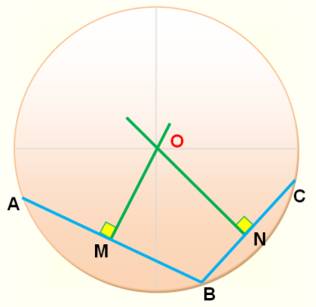
Trois points	Trois points non alignés. Médiatrices M1 et M2 des segments AB et BC. Alors: OA = 0B OB = OC Et OA = OC Le point O est aussi sur la médiatrice du segment AC.
	Il existe un point et un seul à égale distance de trois points non alignés. Ce point est l'intersection des médiatrices des trois côtés du triangle formés par ces trois points.

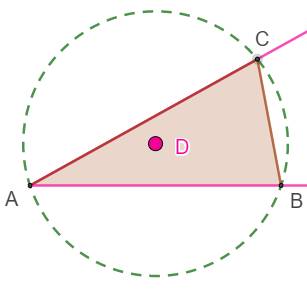
Triangle	Le point O sur la médiatrice OC' de AB est à égale distance R des points A et B. Le point O sur la médiatrice OB' de AC est à égale distance R des points A et C.
	Le point O sur la médiatrice OA' de BC est à égale distance R des points B et C. Le point O à égale distance de A, B et C est unique et il est le centre du cercle circonscrit du triangle ABC. Voir Points du triangle

Cercle	Comment trouver centre du cercle? Choisissez trois points sur le cercle: A, B et C Dessinez deux segments [AB] et [BC]. Tracez les médiatrices; elles se coupent en O, le centre du cercle
	Suite en Cercle

Propriétés

La médiatrice d'un segment est l'axe de symétrie de ce segment. Elle partage le plan en deux demi-plans. Les médiatrices d'un triangle sont concourantes en un point qui est le centre du cercle circonscrit du triangle.

Anglais

Perpendicular bisector of a line segment AB is the straight line perpendicular to AB through the midpoint of AB. Construction of the perpendicular bisector of a line The geometric method of bisecting a line is based upon the fact that all points equally distant from the ends of a straight line lie on the perpendicular bisector of the line. If a line AB is to be bisected, the compass is opened until the distance between its points is more than half as long as AB. Then a short arc is drawn above the approximate center of the line and another below, using A as the center of the arcs’ circle. Two more short arcs are drawn, one above and one below the approximate center of line AB, this time using B as the center of the arcs’ circle. The two arcs above line AB are extended until they intersect, forming point C, and the two arcs below line AB intersect to form point D. The line joining point C and point D is the perpendicular bisector of line AB.

En savoir plus

Bissection Bissection et trisection Cercle défini par une sorte de U Constructions élémentaires: médiatrice Diagramme de Voronoï – Médiatrices en pleine action! Éléments remarquables du triangle Égalités Géométrie – Index Géométrie – Les bases Médiatrice du pentagone et nombre d'or Médiatrices et distances Milieu d'un segment Partage du cercle en parts égales Triangles Triangles - Index

Construction
On donne un des angles du triangle et D le point de concours des médiatrices. Compléter le triangle. Construction 1. Angle ABC, donné. 2. Point D, intersection des médiatrices, donné. 3. Cercle (D, DA). Intersections B et C 4. Le triangle ABC est le triangle cherché. Le cercle en pointillés verts est le cercle circonscrit au triangle ABC.

Amusement: médiatrice et complexes
Question Deux points A (1,0) et B (0,i); Donnez l'équation de la médiatrice du segment AB en version nombres complexes. Solution M est sur la médiatrice de AB, ce qui revient à écrire MA = MB. Or en notation complexe, avec M d'affixe z: L'égalité MA = MB implique que les modules des vecteurs correspondants sont égaux: 1 - z = i - z

Étude de médiatrices
Énoncé Triangles quelconques ABC et BCD. Médiatrices des côtés non communs. Intersections E et F. Point E sur médiatrice de BC E sur médiatrice de AB => AE = EB E sur médiatrice de AC => AE = EC Alors: AE = EB = EC Le point E équidistant des points B et C est sur la médiatrice de BC Même raisonnement pour F qui est sur la médiatrice de BC Position relative de EF et BC Les points E et F sont sur la médiatrice de BC: la droite EF est la médiatrice de BC; et EF est perpendiculaire à CD.

Coordonnées du centre du cercle circonscrit
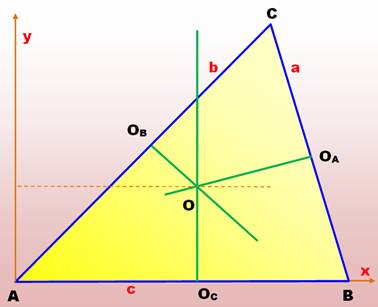
Quelles sont les coordonnées du point O? Avec AT l'aire du triangle ABC (voir formules de Héron). Même formules avec permutations pour les autres médiatrices.

Voir Calculs pour l'orthocentre / Droite d'Euler

Cette page

http://villemin.gerard.free.fr/Referenc/Vocabula/GlosM/Mediatri.htm