géométrie élémentaire: égalité, ressemblance, différence

NOMBRES - Curiosités, théorie et usages Accueil / Dictionnaire / Rubriques / Index / Atlas / Références / Nouveautés ORIENTATION GÉNÉRALE - *M'écrire* - Édition du: 09/02/2012
Débutants Géométrie	Géométrie ÉLÉMENTS de base				Glossaire Géométrie
	Généralités
		Point	Droite	Plan
		Parallèle	Perpendiculaire
		Égalité	Distance	Angle
		Sommaire de cette page >>> Ressemblance et égalité >>> Triangles >>> Isométrie

ÉGALITÉ en GÉOMÉTRIE

Le mot qui convient est ISOMÉTRIE (Grec: Iso égal et métron mesure).

L'outil qui permet de constater l'égalité de deux figures géométriques est la superposition après déplacement adéquate de l'une des figures. On peut déplacer une figure en la faisant

glisser, pivoter ou en la retournant.

L'égalité de deux figures géométriques porte sur les figures à une dimension ou plus:

Égalité de deux figures géométriques

Deux figures géométriques du plan sont égales si on peut les superposer par GLISSEMENT ou par RETOURNEMENT

Rappel

Le glissement simple est appelé translation.

Mais le mot glissement recouvre à la fois la translation et la rotation.

Le retournement (miroir) est une symétrie axiale.

Ces opérations sont des déplacements appartenant à la famille plus générale des transformations des figures géométriques.

RESSEMBLANCE et ÉGALITÉ
Ressemblance	Mêmes allures.
Superposables	Confondus lorsque mis l'un sur l'autre. Mêmes formes et mêmes dimensions.
Équivalents	Mêmes propriétés. Rien ne permet de distinguer l'un de l'autre.
Symétriques	Superposables, pas nécessairement par glissement. Effet miroir possible. Nécessité de retourner l'objet en utilisant l'espace (3D).
Égaux Isométriques	Équivalence en géométrie plane. Superposables par glissement.
Différents	Lorsque non égaux.
Identiques	Que lorsqu'on parle du même objet. Il est "égal" à lui-même.
Distincts	Deux objets séparés, indépendants. Ils peuvent être égaux ou non.

TRIANGLES – Cas d'égalité des triangles
Deux triangles sont égaux (isométriques) ou de même forme ou congruentes *si et seulement si* l'une des trois conditions suivantes est remplie:
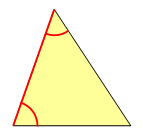
un angle égal compris entre deux côtés respectivement égaux
un côté égal adjacent à deux angles respectivement égaux
trois côtés respectivement égaux

À bien noter
Deux triangles sont égaux (congrus) si 3 éléments sont égaux dont au moins un côté.	3 angles égaux (congrus) ne donnent pas forcément deux triangles égaux: ils sont semblables. Voir Triangles semblables
Remarque: Congruent est le mot mathématique pour signifier que deux figures sont identiques en forme et dimensions – DicoMot