Triangles héroniens à 120°

Édition du: 27/03/2025

Faites un double-clic pour un retour en haut de page

Triangles héroniens à 120°

Triangles ayant un angle de 120° et dont les côtés sont des nombres entiers.

Où l'on trouve une sorte de formule de Pythagore

Sommaire de cette page

>>> Loi des cosinus avec angle de 120°

>>> Triangles héroniens à angle de 120°

>>> Relation au carré: puissance 4

Débutants

Nombres

Glossaire

Nombres

Loi des cosinus avec angle de 120°		haut
Cosinus 120° Avec un angle de 120°, le cosinus vaut -0,5. La loi des cosinus dans un triangle quelconque implique le double du cosinus, soit la valeur -1. Nous disposons d'une formule qui, si les côtés a et b sont deux nombres entiers, le troisième côté est aussi un nombre entier.
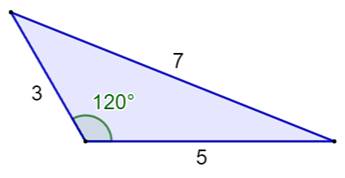
Plus petit triangle On obtient le plus petit triangle avec a = 3 et b = 5. Alors: 3² + 5² + 3 × 5 = 49 = 7² Le troisième côté vaut: 7, un nombre entier.

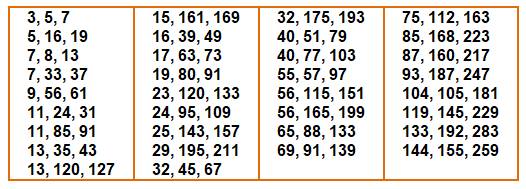
Triangles héroniens à angle de 120°		haut
Table Les 34 triangles avec des côtés a et b jusqu'à 200. Ce sont les triangles primitifs. Chacun peut être décliné à l'infini en multipliant tous les côtés par un facteur k.
Formule Ces triplets sont engendrés en prenant m et n premiers entre eux et avec ces trois formules. Exemple m = 5 et n = 1 a = 25 – 1 = 24 b = 2 × 5 + 1 = 11 c = 1 + 5 + 25 = 31	a = m² – n² b = 2mn + n² c = m² + mn + n² Note: le nombre c est calculé à partir de a et b avec la formule indiquée.

Relation au carré: puissance 4

haut

Prenons le carré de notre formule au carré et doublons le résultat.

Bilan: le double de ce type de carré est exprimable par une somme de trois puissances quatrièmes.

Dans certains cas, le carré peut cacher une puissance quatrième

Exemples

a = 3 et b = 5

9 + 25 + 15 = 98

2 x 98² = 3⁴ + 5⁴ + 8⁴ = 4 802

7⁴ + 8⁴ + 15⁴ = 2 × 169² = 13⁴ = 57 122

11⁴ + 24⁴ + 35⁴ = 2 × 961² = 31⁴ = 1 847 042

Haut de page (ou double-clic)