NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/04/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Triangles
Débutants Triangle	TRIANGLES RATIONNELS			Glossaire Triangle
INDEX Triangle Ésotérisme	Isiaques	Héroniens	Congruents
		Sommaire de cette page >>> En bref – Les mensurations >>> Triangle sacré >>> Relations remarquables avec 3, 4 et 5 >>> Triangles en (3, 4, 5) >>> Triangle isiaque >>> Triangle des jardiniers >>> Triangles voisins

TRIANGLE 3 - 4 - 5 ou triangle SACRÉ (d'Isis) ou triangle ISIAQUE ou triangle de PYTHAGORE ou triangle des ARPENTEURS ou triangle des JARDINIERS

Voir Théorème de Pythagore / Nombres imaginaires

En bref – Les mensurations

Triangle rectangle isiaque: 1 – Rayon du cercle inscrit; 2 – Diamètre de ce cercle; 3 – Petit côté de l'angle droit; 4 – Grand côté de l'angle droit; 5 – Hypoténuse et rayon du cercle circonscrit; 6 – Aire du triangle; 7 – Longueur des deux côtés de l'angle droit; et π – Aire du cercle inscrit

Voir Brève 57-1122 / Relations entre Pi et les triplets de Pythagore

Racine de 5 et triangle isiaque

Voir Brève 58/1159

Introduction au triangle sacré
Ce triangle rectangle était bien connu de Pythagore, initié à la mythologie Égyptienne et à la cosmogonie de Sumer et de Babylone. Le carré de l'hypoténuse est égal à la somme des carrés des côtés. 5² = 4² + 3² Avec, ici, une superbe coquetterie pour ce triplet de Pythagore; les trois nombres sont consécutifs. De plus, l'aire de ce triangle vaut 6 et son périmètre 12, le double. Le nombre 7 prend la suite comme somme des longueurs des côtés de l'angle droit.
The triangle shown has its sides in the ratio 3 to 4 to 5 Any triangle with its sides in this ratio is a right triangle 3 – 4 - 5 is one example of the many Pythagorean triples
On peut pousser les relations avec les nombres jusqu'à 12, le 11 étant absent.

Voir Jeux – Faire les nombres successifs sous contraintes

Un autre tel triplet ?

On cherche trois nombres consécutifs avec cette configuration en carrés:

(n – 1)² + n² = (n + 1)²

n² – 2n + n² = n² + 2n + 1

n² – 4n = n (n – 4) = 0 => n = 0 ou 4

Seule solution non triviale:

3² + 4² = 5² = 25

Sur le même modèle, la somme suivante est:

10² + 11² + 12² = 13² + 14² = 365

Voir Suite de ces égalités de sommes de carrés consécutifs

Relations remarquables avec 3, 4 et 5
Relations dans le triangle (3, 4, 5) 3² + 4² = 5² = 25 3 × 4 = 2,4 × 5 = 12 3² = 5 × 1.8 = 9 4² = 5 × 3,2 = 16 2,4² = 3,2 X 1,8 = 5,76 4² – 3,2² = 3² – 1,8² = 2,4² = 5,76 Voir Poster triangle rectangle

Relations les nombres (3, 4, 5)
Base horaire	3 + 4 + 5	= 12
Base angulaire (Babylone)	3 x 4 x 5	= 60
Nombre nuptial	3² x 4² x 5²	= 3 600
Triplets de Pythagore	3² + 4²	= 5² = 25
Tête d'une suite d'égalités et nombres hexagonaux	3² + 4² 10² + 11² + 12² …	= 5² = 13² + 14² …
Nombre du domaine bestial	3^3 + 4^3 + 5^3	= 6^3 = 6 x 6 x 6 = 216
Curiosité	3^3 x 4^3 x 5^3	= 216 000

Formule de perfection cubique
Puissance 2	3^2 + 4^2 + 5^2	= 50	= 1² + 7² = 5² + 5²
Puissance 3	3^3 + 4^3 + 5^3	= 216	= 15² - 3² = 21² - 15² = 29² - 25² = 55² - 53²
Puissance 4	3^4 + 4^4 + 5^4	= 962	= 1² + 31² = 11² + 29²
Puissance 5	3^5 + 4^5 + 5^5	= 4 392	= 6² + 66² = 79² - 43² = 131² - 113² = 189² - 177² = 369² - 363² = 551² - 547²
Puissance 6	3^6 + 4^6 + 5^6	= 20 450	= 1² + 143² = 41² + 137² = 85² + 115²
Puissance 7	3^7 + 4^7 + 5^7	= 96 696	= 311² - 5² = 339² - 135² = 385² - 227² = 525² - 423² = 745² - 677²
Puissance 8	3^8 + 4^8 + 5^8	= 462 722	= 41² + 679² = 259² + 629² = 299² + 611² = 449² + 511² = 481² + 481² = 2 x 481²

Voir Pépites / Nombre 216

Relation avec Pi et le nombre d'or

a = 3, b = 4 et c = 5

Une approximation classique de la constante Pi

Valeurs exactes du nombre d'or et de son inverse

Le triplet de nombres consécutifs peut s'écrire:

(n – 1)² + n² – (n + 1) = n² – 4n = n (n – 4) = 0

Solution n = 0 et le triplet est: (-1)² + 0 = 1² (trivial

Solution n = 4 et le triplet est: 3² + 4² = 5², le triplet isiaque.

Formules proposées par Giuseppe-Luciano Ferrero

Triangles en (3, 4, 5)
Les longueurs des côtés d'un triangle rectangle sont trois nombres en progression arithmétique. Montrer que les longueurs sont dans le rapport (3 : 4 : 5).	Trois nombres en progression arithmétique: (n – e) , n et (n + e) Théorème de Pythagore: (n – e)² + n² = (n + e)² n² – 2ne + e² + n² = n² + 2ne + e² n² – 4ne = 0 n (n – 4e) = 0 n = 4e Longueurs des côtés: 3e, 4e, 5e

TRIANGLE ISIAQUE

Triangle en l'honneur de trinité égyptienne Osiris, Isis et leur fils Horus.

3 le mâle;

4 la femelle; et

5 le fruit de leur union.

Placé dans les pyramides des Égyptiens, plus exactement dans la chambre funéraire du pharaon.

Chez les Grecs, il paraît avoir été considéré comme le symbole du mariage.

Plutarque le dénomme le plus beau des triangles et rapporte que c'est à lui que les Égyptiens assimilaient la nature de l'univers

Livre de Isis à Osiris Chapitre 56

Manuscrit égyptien découvert en 1929

Des variantes du triplet (3, 4, 5)

ISIAQUE. adj. Qui appartient à Isis, divinité égyptienne.

La table isiaque, célèbre monument de l'antiquité sur lequel sont représentés les mystères d'Isis. Académie française

ISIS Déesse de la fertilité et de la maternité

Première fille du dieu Keb (Terre) et de la déesse Nut (Ciel)

Sœur et femme d'Osiris, le juge des morts

Mère d'Horus (Jour)

Voir Don de Thot

Triangle des ARPENTEURS ou des JARDINIERS
Moyen pratique pour construire un angle droit. On dispose d'une corde à 13 nœuds régulièrement espacés (12 intervalles!) un pieu planté à l'endroit où l'on souhaite créer l'angle droit; on y place le nœud 5; une personne au nœud 8 pour matérialiser un des angles; et une deuxième personne pour fermer le dernier angle aux nœuds 1 et 13.
On note que seuls les nœuds 5 et 8 auraient suffi; les autres ont un intérêt à la construction, pour faciliter le respect de l'unité de distance. Évidemment, il s'agit d'une construction approximative: - Positionnement des deux personnes; - Élongation de la corde; - Précision du placement des nœuds; - Sans parler de l'humidité du temps …

Voir Triangle du jardinier

Triangles voisins
Triangle de Pythagore Il est clair que tout triangle dans les proportions 3, 4 et 5 est aussi un triangle de Pythagore (ou isiaque): 5k² = 4k² + 3k² Exemple avec k = 2: 10² = 8² + 6² Les angles se calculent au moyen de la trigonométrie: α = arcsin (3/5 ) = 36, 87 ° β = 90 – α = 53, 13 ° Aire du triangle: A = 3k . 4k / 2 = 6k² Périmètre du triangle: P = 3k + 4k + 5k = 12k

Triangle 45 ou demi-carré Triangle rectangle ayant un angle de 45 ° L'autre valant également 45 ° (90 – 45) C'est évidemment; un triangle isocèle; rectangle isocèle même. La longueur de l'hypoténuse se calcule avec le théorème de Pythagore: h²= k² + k² = 2k² h = k √2 Aire du triangle: A = k . k / 2 = ½ k² Périmètre du triangle: P = k + k + √2k = k (2 + √2)

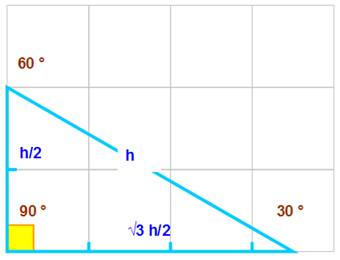
Triangle 30 – 60 ou triangle des écoliers (celui des équerres classiques) ou triangle hémi-équilatéral (ou demi-équilatéral) Triangle rectangle ayant un angle de 30 °. L'autre valant 60 ° (90 – 30). Triangle remarquable car un des côtés mesure la moitié de l'hypoténuse. Tout cela du fait que: sin 30° = 1/2 L'autre côté mesure: h .cos 30° = h . √3/2 Aire du triangle A = h/2 . h/ 2 = √3/4 h² Périmètre du triangle P = h + h/2 + √3 h/ 2 = ½ h (3 + √3)

Triangle avec 3 et 4 Triangle rectangle dont l'hypoténuse mesure 4 et l'un des côté 3. Calcul des autres valeurs: arcsin α = 3/4 = 48, 59037… ° β = 90 – α = 41, 40962… ° L3^e côté = 4 sin β = √7 = 2, 64575… On vérifie le théorème de Pythagore: (√7)² + 3² = 7 + 9 = 16 = 4² Curiosité: Cotés de longueur 3 et 4 et 3^e côté de longueur √(3 + 4). Aire du triangle: A = 3√7 / 2 Périmètre du triangle: P = 3 + 4 + √7 = 7 + √7

Voir toutes les formules en Résolution des triangles

Suite	Partage du triangle isiaque en deux parties de même aire et de même périmètre Triangle héroniens Côtés en progression arithmétique Nombre 216 Nombre de Platon Énigme des deux cercles dans le triangle 3-4-5
Voir	Ésotérisme Nombre de la bête Nombres congruents Pépites Pythagore (décade) Résolution des triangles Triangles Triplets de Pythagore
DicoNombre	Nombre 3 Nombre 4 Nombre 5 Nombre 13 Nombre 3 600
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Esoteris/Isiaque.htm