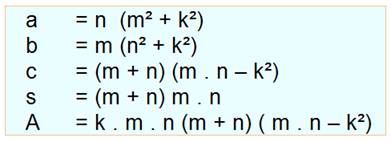|
|||||||||||||||||||||||||||||||||||||
![]()
|
TRIANGLES HÉRONIENS Triangles quelconques dont les mesures sont des nombres entiers ou rationnels; côtés et aire. Notez que: un triangle entier ou héronien (côtés = entiers) et aire entière, son aire est multiple de 6. Historique: Il y a 2000 ans, Héron d'Alexandrie donne un exemple:
a = 13, b = 14 et c = 15 avec une aire de 84. Au XVIIe siècle,
plusieurs mathématiciens reprendront les travaux: François Viète, C.G. Bachet
and Frans van Schooten jr. Au XIXe, ils font l'objet de jeux. En
1934, Dickson fait le point sur ces triangles. |
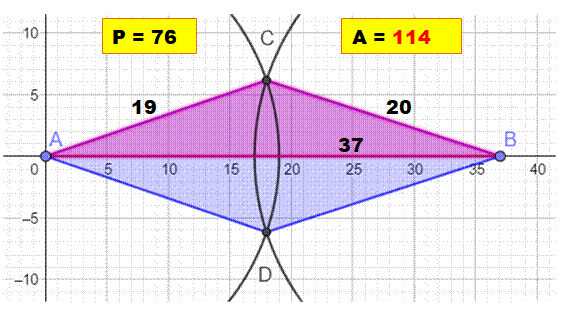
Exemple
|
Les
triangles ABC et ABD sont héroniens. En effet: Les
longueurs des cotés sont entières: (19, 20 et 37)
Le
demi-périmètre vaut s = ½ (19 + 20 + 37) = 38 L'aire
se calcule avec la formule
de Héron:
Et, A = 114, un nombre entier. Notez la construction
du triangle
quelconque: tracez AB de longueur 37, puis deux cercles de centre A et B
de rayon 19 et 20. |
Voir Nombre
114
![]()
|
|
||
|
Comment
construire de tels triangles héroniens?
P
= 2 s = a + b + c, le périmètre. Le carré de l'aire du triangle est égale à: A² = {
s(s – a) (s – b) (s – c) } Exemple avec le triangle isocèle 5 – 5
– 6 P = 5 + 5 + 6 = 16 s = 8 A² = 8 x 3 x 3 x 2
= 16 x 9 A = 4 x 3 = 12 |
|
|
Héroniens remarquables – Integer triangles
|
Quantité de triangles de périmètre P pour P de 3 à 20
La suite de ces nombres est nommée suite d'Alcuin Suite OEIS
A005044 Formule
Lire: plancher
de n²/48 …) Exemples Il y a quatre triangles
héroniens de périmètre égal à 11. Au total, il y a quinze
triangles à côtés entiers (héroniens) ont un périmètre inférieur ou égal à
11. Même valeur pour le périmètre et pour l'aire Seuls cinq triangles à côtés entiers ont la même valeur pour le
périmètre et l'aire: Equable triangles: area equals its perimeter. |
|
|
|
|
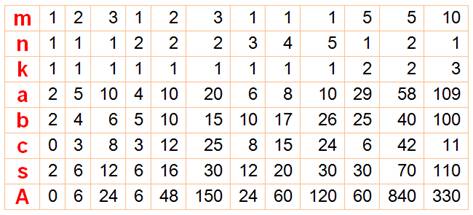
Cas
générique
Voici
quelques exemples numériques
Les
premiers triplets dans l'ordre de la longueur maximale (3, 4,
5), (5, 5, 6), (5, 5, 8), (6, 8, 10), (10, 10, 12), (5, 12,
13), (10, 13, 13), (9, 12, 15), (4, 13, 15), (13,
14, 15), (10, 10, 16), ... Valeurs pour a, b et c <101 Voir table |
|
|
|
|
|
Ce
qui implique que le point (sin |
|
Voir Trigonométrie
/ Cercle unité et
Suite en Nombre
t-congruent
|
Cette suite de neuf valeurs est une suite héronienne trouvée par Paul Yiu,
K. R. S. Sastry and Shanzhen Gao en 2007:
|
Voir Heron
Sequences and Their Modifications / OEIS
A134587
|
On ne sait pas s'il existe des triangles héroniens avec médianes
entières. On ne sait pas s'il existe des triangles héroniens de Fibonacci
(côtés = nombres de Fibonacci), autre que le triangle (5, 5, 8).
|
![]()
|
Suite |
|
|
Héron |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Esoteris/Heronien.htm |
![]()