Triangle équilatéral entier

Édition du: 11/03/2024

INDEX Triangle équilatéral Triangle Géométrie	Triangles entiers
	Triangles	Côtés entiers	Pythagore	Même aire
	Isiaque	Entiers spécifiques	Congruents	Entier équilatéral
	Fibonacci	Héron

Triangle équilatéral entier

à distances internes entières

Comment trouver un point interne au triangle équilatéral tel que les distances de ce point aux sommets soient des nombres entiers ?

Pas simple, du moins il a fallu un peu d'astuce géométrique pour arriver à la solution: une rotation appropriée.

Sommaire de cette page

>>> Triangles ENTIERS et distances entières

>>> Distances entières à un point interne

>>> Triangle équilatéral entier et distances entières à un point interne

>>> Recherche paramétriques

Débutants

Triangle

Glossaire

Triangle

Triangles ENTIERS et distances entières			haut
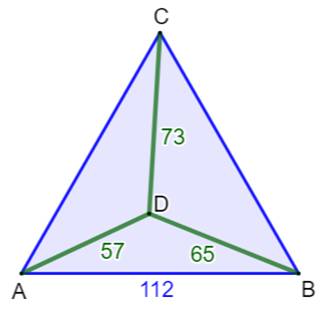
Approche Les triangles équilatéraux de côté t, avec t un entier, sont des triangles entiers. Trop commun! Oui, alors … On cherche plutôt des distances entières dans le triangle équilatéral: Par exemple: trouver un point interne (D) tel que la distance de ce point aux sommets soient des nombres entiers. Il existe une infinité de ces triangles, même si leur recherche est difficile. Celui de cette figure est la plus petite solution.		Exemple de triangle équilatéral entier à distances internes entières
Héronien ? Jamais	Pour être héronien, le triangle équilatéral doit avoir des côtés entiers et une aire entière. Or, l'aire du triangle équilatéral est égale à: Si c est un nombre entier, l'aire est nécessairement irrationnelle.

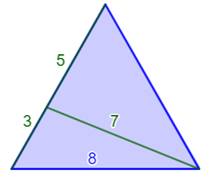
Distances entières à un point interne

haut

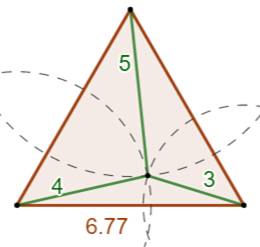
Triangle équilatéral avec points entiers

On cherche le côté (entier ou non) d'un triangle équilatéral dont un point interne est éloigné de 3, 4 et 5 des sommets. En l'occurrence trois nombres entiers.

Calcul avec (3, 4, 5)

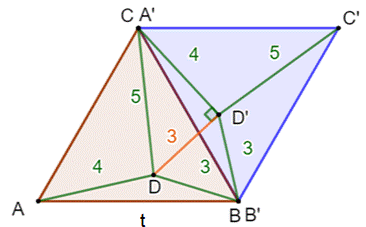
Astuce! En fait, la puce à l'oreille est la présence des trois nombres (3, 4, 5) qui font penser à un triplet de Pythagore.

On procède à une rotation négative (-60°) de la figure autour de B qui produit l'image du triangle en bleu.

L'angle DBD' est égal à l'angle ABC, soit 60°. Le triangle BDD' a un angle de 60° et deux côtés égaux (DB et D'B'), il est équilatéral et DD' = 3.

Le triangle CDD' (3, 4, 5) est un triangle de Pythagore et l'angle CD'D est droit.

Alors, l'angle CD'B = 90 + 60 = 150°.

Dans le triangle CD'B, on applique la loi des cosinus:
CB² = t² = 3² + 4² – 2 × 3 × 4 × cos150°

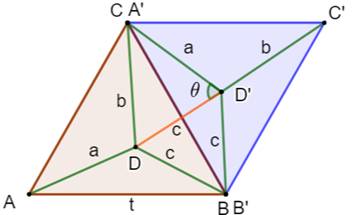
Cas général avec (a, b, c)

Notez que le triangle BDD' est toujours équilatéral (60° en B et BD = B'D' = c); conséquence: DD' = c.

Même principe de calcul que ci-dessus, en constatant au départ que:
(

Formule finale (calcul ci-dessous):

Triangle équilatéral avec P(3, 4, 5)

Triangle initial ABC et rotation (A'B'C') de - 60°

Cas général

Calcul de la formule

Triangle équilatéral entier et distances entières à un point interne		haut
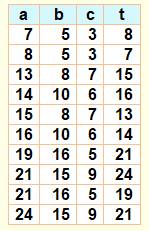
Méthode Nous disposons d'une formule qui, à partir de trois distances entières (a, b, c) permet de calculer le côté (t) du triangle équilatéral. Pour trouver, des longueurs de côté en nombres entiers, une exploration systématique par programmation est nécessaire. Premier résultats La figure montre les deux premières solutions (7, 5, 3 donne t = 8 & 8, 5, 3 avec t = 7) Deux cas non recevables pour cause de point D sur le périmètre et point D externe. Le tableau indique les quelques résultats suivants.
Conditions sur les distances L'exploration est poursuivie en imposant que chaque côté < t somme de deux côtés > t La figure montre les deux premières solutions (57, 65, 73 et t = 112 & 73, 88, 95 et t = 147 (solutions avec côté les plus petits). Le tableau indique les quelques résultats suivants pour a, b et c jusqu'à 500.	43, 147, 152, 185 43, 248, 285, 287 49, 285, 296, 331 57, 65, 73, 112 73, 88, 95, 147 86, 294, 304, 370 95, 312, 343, 403 97, 185, 208, 273 111, 221, 280, 331 114, 130, 146, 224 127, 168, 205, 283 129, 441, 456, 555 146, 176, 190, 294 147, 377, 437, 520 152, 343, 387, 485 152, 365, 497, 507 171, 195, 219, 336 194, 370, 416, 546 219, 264, 285, 441 228, 260, 292, 448 247, 408, 485, 637 254, 336, 410, 566 255, 343, 473, 592 285, 325, 365, 560 285, 464, 469, 691 292, 352, 380, 588 296, 315, 361, 559 323, 392, 407, 645 342, 390, 438, 672 365, 440, 475, 735

Voir Brève 840

Recherche paramétriques

haut

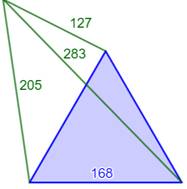
Méthode

En 1999, Arnfried Kemnitz a trouvé une solution paramétrique produisant une infinité de solutions (mais pas toutes).

On se donne les paramètres u et v (u > v) et on calcule:

m = 2(u² – v²)

n = u² + 4uv + v²

a = m² + n²

b = m² – mn + n²

c = m² + mn + n²

On note que a = (b + c) / 2

t = 8(u² – v²) (u² + uv + v²)

(a, b, c) sont les longueurs (verts)

(t) est la longueur du côté du triangle équilatéral

205, 127, 283, 168

740, 388, 1092, 832

1469, 1099, 1839, 760

1989, 999, 2979, 2520

3280, 2032, 4528, 2688

5525, 4503, 6547, 2072

4420, 2212, 6628, 5952

6525, 3627, 9423, 6552

9860, 6852, 12868, 6272

14965, 12787, 17143, 4392

Haut de page

Retour	*Voir* Haut de page Triangle équilatéral
Suite	Table des triangles entiers (pdf) Triangles rectangles entiers – de Pythagore Triangles rectangles particuliers Énigme des cruches d'huile d'Alcuin (partage)
Voir	Losange Puzzle chinois Rectangle Triangle – Index Types de triangles
Site	Perfect Rational Triangle – Epstein Junkyard – Randall
Livre	Aha! Solutions – Martin Erickson – Mathematical Association of America – 2009
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TrgequiE.htm