|
Édition du: 24/10/2024 |
|
INDEX |
Échecs – Cavalier |
||
|
|
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
♞ PÉRIPLE du CAVALIER ♞ Problème du cavalier, algorithme du cavalier, cavalier
d'Euler Un problème très répandu
consiste à faire parcourir tout l'échiquier au cheval en passant par toutes
les cases et une seule fois. Il est intéressant de commencer par un échiquier
réduit et de rechercher les cas possibles ou impossibles. Les recherches sur ce sujet
sont sans doute du même ordre que celles sur les carrés
magiques. Experts
concernant ce sujet Ce sujet a passionné quantité de mathématiciens
et amateurs >>>. George
Jelliss a minutieusement compilé tout ce qu'il faut savoir sur le périple
du cavalier.
|
||
|
|
Sommaire de cette page >>> Déplacement et menace du cavalier >>> Types de périples >>> Périple du cavalier – Petites échiquiers >>> Quantité de périples >>> Périples sur échiquier classique 8×8 >>> Périples sur échiquier classique 11×11 >>> Échiquier rectangulaire |
Débutants Glossaire |
Anglais: The move of a
chess knight, knight's tour / The knight tour problem
|
Exemple de mouvement du cavalier
Notez qu'à
chaque mouvement du cavalier, la couleur de la case change. |
Menace du cavalier
|
|
|
À partir des échiquiers de taille 5, la quantité de
possibilités de périples du cavalier sont si nombreuses que l'on cherche des
configurations particulières.
|
|
|
Voir Exemples de périples selon la taille de l'échiquier
|
Principes Le cavalier effectue un voyage lui faisant
visiter chacune des cases une seule fois. Lorsque le cavalier revient à son point de
départ, on dit que le parcours est fermé. Les mouvements sur l'échiquier n×n sont notés à
partir de 0 sur la case de départ jusqu'à n² – 1 sur la case d'arrivée. La quantité de solutions croit rapidement avec la
taille de l'échiquier. Même trouver une solution s'avère difficile, pourtant
certains se donnent des contraintes supplémentaires pour sélectionner des cas
notables. Par exemple, faire figurer les carrés des numéros de mouvement sur
une figure géométrique. Ce jeu peut être prolongé sur des échiquiers
rectangulaires. |
Exemple
|
||
|
Échiquier 2 × 2 |
Le cavalier ne peut pas se déployer. Impossible. |
||
|
Échiquier 3 × 3 |
Le cavalier ne peut pas atteindre la case du
milieu. Impossible. Voir liberté de mouvement |
||
|
Échiquier 4 × 4 |
Impossible. Voir liberté de mouvement |
||
|
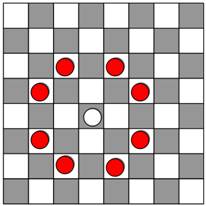
Échiquier 5 × 5 |
Possible En rouge, le début du parcours de 1 à 9. Mais impossible de revenir au point de départ à la
fin du périple: parcours non fermé. |
||
|
Échiquier 3 × 4 |
Rectangle le plus petit permettant le périple du
cavalier. Mais non-fermé. |
||
|
Tableau En rouge, les plus petites surfaces possibles. En bref Il existe une solution pour tout échiquier rectangulaire dont la
longueur et la largeur sont supérieures ou égales à 5. |
|
|
|
Quantité de solutions en parcours
ouverts |
Liste pour n à partir de 1 1, 0, 0, 0, 1728, 6637920,
165575218320, 19591828170979904, … Ces quantités incluent les trajets allers et retours ainsi que toutes
rotations et réflexions. OEIS A165134 - Number of directed
Hamiltonian paths in the n X n knight graph or Number of knight's paths
visiting each square of an n X n chessboard exactly once. |
|
|
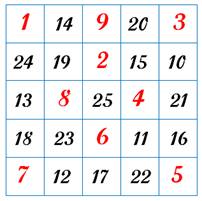
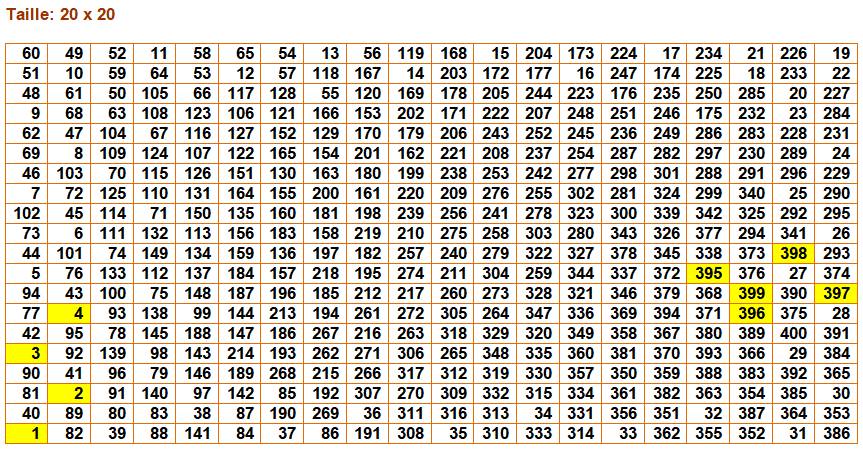
Cas de n = 5 Calculs par Gheorghe Coserea en 2016 Le premier a été publié par Euler |
1728 périples du cavalier possibles avec un échiquier de 5×5 dont les cases
de départ sont les quantités indiquées dans ce tableau:
ll y a 112 périples géométriquement distincts. Ils ont tous un début
ou une fin dans un coin. Ils sont tous ouverts comme pour tous avec une
taille impaire. Parmi eux, 8 sont symétriques. |
|
|
Cas des parcours fermés |
Schwenk a prouvé (1991) que tout échiquier m × n avec m ≤ n, un périple
fermé est toujours possible sauf si l'une des conditions suivantes est
réalisée:
|
|
|
Principes Il s'agit de parcourir toutes les cases de
l'échiquier en faisant progresser le cavalier selon son déplacement
classique. On ne connaît pas le nombre de solutions: c'est
plusieurs millions. En voici deux qui présentent des symétries: Voir Graphes
– Index |
Euler en 1759 Chaque couple de nombres symétriques par rapport
au centre présente une différence de 32.
|
|
|
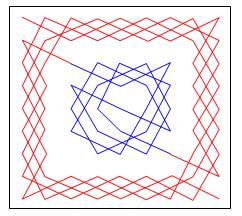
Dessins avec les carrés La diversité des possibilités sur un échiquier de
taille 11 est telle qu'Awani Kumar (Lucknow, Inde) s'est amusé à compiler
toute une série de périples tels que les nombres carrés forment une figure. Exemples
Son travail "Figured tours of knight on
11x11 Board" n'est malheureusement pas facilement accessibles sur
Internet. |
|
|
Des critères semblables existent pour les
périples ouverts. |
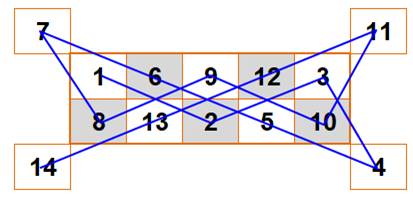
Périple ouvert sur 5×4
|
||
|
Périple fermé à tout prix Comme la réalisation d'un périple n'est pas
toujours possible sur un échiquier rectangulaire le jeu consiste à déterminer
le minimum de cases à ajouter pour rendre le trajet possible. |
Extensions pour un périple fermé
sur 5×2
|
||
![]()
Quelques exemples de périples sur échiquier
carrés




![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()