|
Édition du: 02/04/2024 |
|
INDEX |
Échecs – Cavalier |
||
|
|
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
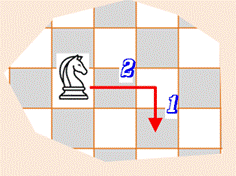
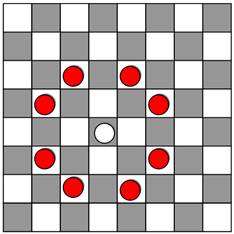
♞ ÉCHECS & CAVALIER ♞ Le mouvement particulier des
cavaliers sur l'échiquier donne l'occasion à de multiples jeux et défis. Maîtres concernant
ce sujet Martin Gardner, célèbre pour tous ses développements sur les jeux mathématiques, et Solomon W. Golomb célèbre pour ses
recherches sur les polyominos et autres pentominos. George
Jelliss a compilé tout ce qu'il faut savoir sur le périple
du cavalier. |
||
|
|
Sommaire de cette page >>> Types de défis à
propos des cavaliers >>> Mouvement du cavalier >>> Vocabulaire |
Débutants Glossaire |
Anglais: The move of a
chess knight, knight's tour
|
# |
Type |
Description |
Lien |
|
1 |
D'une
case à une autre |
Combien de mouvements |
|
|
1 |
Chemin le
plus court de coin à coin |
Minimum de mouvements pour rejoindre le coin
opposé |
|
|
1 |
Diamètre |
Distance la plus grande parmi toutes les
distances pour aller de chaque case à chacune des autres |
|
|
1 |
Parcourir toute les cases une seule fois |
||
|
1 |
Quantité de cases maitrisée après k mouvements. |
||
|
q |
Combien de cavaliers au maximum sur l'échiquier
sans que l'un menace les autres |
||
|
q |
Domination
de l'échiquier par q cavaliers |
Combien de cavaliers au minimum pour dominer
toutes les cases de l'échiquier |
|
|
1 |
Quels sont les chemins possibles du cavalier sur
un échiquier |
||
|
q |
Combien de mouvements au minimum pour inverser
les blancs et les noirs |
||
Voir Menace du cavalier
|
Français: cavalier ou cheval Anglais: knight Allemand: Springer Espagnol: caballo Russe: KOHb (prononciation: kon') Culture: les mots cavalier, fou, roi … sont des méronymes du mot échecs. |
|
The
classic puzzle of finding a closed knight’s tour on a chessboard consists of
moving a knight from square to square in such a way that it lands on every
square once and returns to its starting point. |
Voir
Anglais pour le bac et pour les affaires
Pièces des échecs
selon les langues
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()