NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 22/08/2013

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                               

     

Algèbre

 

Débutants

Équations

ÉQUATIONS

du 2e degré

 

Glossaire

Équations

2e degré

 

 

INDEX

Équations

 

Introduction

Résolution graphique

Solutions entières

Somme et produit

Résolution simple

Nombres

Historique

Résolution générale

Applications

 

Sommaire de cette page

 

>>> Analogie géométrique

>>> Résolution géométrique

>>> Variante en croix

>>> Interprétation géométrique

>>> Résolution graphique de Descartes

 

 

 

 

ÉQUATIONS du 2e degré

 ou Équation quadratique

 

 Voyez cette résolution graphique (qu'elle est belle ! ). Bien comprise elle révèle le secret de la résolution de l'équation du deuxième degré.

 

 

 

 

ANALOGIE GÉOMÉTRIQUE

 

*      Nous partons de l'équation:  x² + bx  = c

*      Notre défi:

*       trouver un carré x² tel que

*       associé au rectangle b.x,

*       la surface totale soit c.

 

 

*      L'astuce de la démonstration figurative consiste à couper le rectangle en deux sur lequel on va pour former un nouveau carré plus grand.

 

 

 

 

 

RÉSOLUTION – Géométrique

 

*      Les anciens avaient imaginé une méthode graphique pour résoudre l'équation du deuxième degré x² + bx = c

 

 

*      Sur la figure présentée ci-dessus, on fait basculer un demi-rectangle (flèche bleue) en s'aidant du dessin du carré de côté b/2.

 

*      La surface de l'équerre est la somme de trois surfaces:

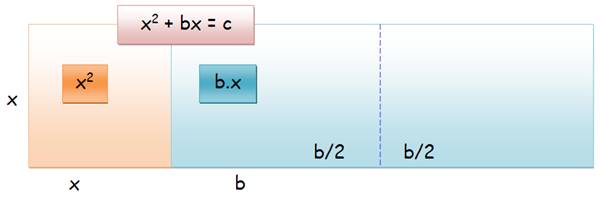
x² + x.b/2 + x.b/2 = x² + bx = c

Effectivement la surface de l'équerre vaut c.

 

*      La surface de cette équerre est aussi égale à celle du grand carré diminuée de celle du carré vert:

c = (x + b/2)2 – (b/2)2

*      Qui devient:

(x + b/2)² = c + (b/2)²

 

 

*      Nous obtenons un carré incluant x qui vaut une constante. Ce qui est facile à calculer.

 

Exemple

x² + 2x = 8

Avec notre formule:

(x + 2/2)² = 8 + (2/2)² = 9

(x + 1) = 3

x = 2

Idée

*      Cette méthode graphique qui consiste à matérialiser des carrés est la base de la résolution générale de ce type d'équations.

 

 

 

 

Variante en croix

 

*      Au lieu de prendre la moitié du côté b, nous prenons le quart. Ce qui fait apparaître une forme en croix.

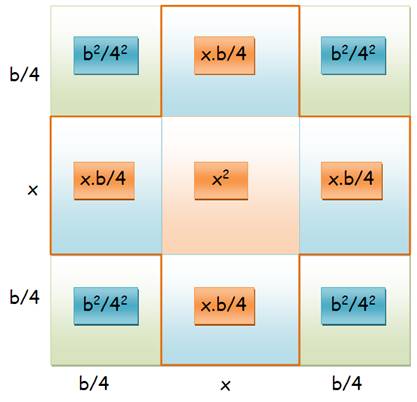
x² + 4 x.b/4 =  (x + 2b/4)² – 4 b²/4²

x² + b.x = c = (x + b/2)² – b²/4

 

 

 

 

INTERPRÉTATION GÉOMÉTRIQUE

 

*      Plus généralement et en géométrie analytique, les solutions de l'équation du second degré, lorsqu'elles sont réelles, représentent les abscisses des points d'intersection avec l'axe des abscisses.de la parabole

y = ax² + bx + c

 

*      Selon que b² – 4 ac est positif, nul ou négatif, il existe deux, un ou aucun point d'intersection.
 

Voir  Illustration

 

 

La célèbre résolution graphique de Descartes

 

Équation

x² – ax – b² = 0

ou

x² = ax + b²

avec a positif

 

Explications

 

 

Illustration

 

 

Rapprochement avec la solution du cas général

 

Voir Descartes / Solution équation du second degré

 

 

 

 

 

Suite

*   Solutions entières

*    Autre exemple  et notations anciennes

*    Voir haut de page

Voir

*    Algorithme d'Héron

*    Équations en poèmes

*    Géométrie – Index

*    Méthode de Newton

*    Système d'équations – Somme100

Cette page

*    http://villemin.gerard.free.fr/ThNbDemo/Eqa2dRGr.htm