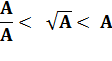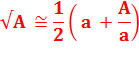|
|||||||||||||||||||||||||||||||||||
![]()
|
CALCUL de la RACINE CARRÉE Algorithme de Babylone ou
Algorithme de Héron Trouver l On trouve
facilement deux nombres encadrant la racine cherchée. La moyenne de ces deux
nombres est une bonne approximation de la racine. Une meilleure valeur est
obtenue en recommençant l'opération… Héron donne sa
méthode à l'occasion du calcul de la racine de 720 = 12 x 5 x 4 x 2. Il
calculait alors l'aire d'un triangle (7, 8, 9) avec la formule qu'il avait trouvée. |
Voir Introduction avec exemple sur
racine de 2
|
Trouvez
n minimum tel que |
|
|
|||
|
Étape
1 |
Littéral |
Exemple |
|
|
|
A |
A
= 10
|
|
|
|
|
A
= 10 (exemple) 3,16
< 10 |
|
|
|
A / A |
10
/ 10 = 1 |
|
|
|
A / A < |
1 < 3,16 |
|
|
|
|
1
< 3,16 < 10 |
|
|
|
r = 1/2 (A + A/A) |
r
=
1/2 (10 + 1) =
5 + 0, 5 =
5, 5 |
|
|
Étape
2 |
|
|
|
|
|
r1 = 1/2 (r + N/r) |
r1
=
1/2 (5,5 + 10/5,5) =
2,75 + 0,909 =
3,659 |
|
|
|
|
rk = 3,16 … |
|
|
RACINE de DEUX – Méthode de Héron ou
Algorithme de Babylone |
|
|
|
Calcul de la racine carrée de A Méthode de calcul par itération: nouvelle
valeur = f(ancienne valeur) En commençant par une valeur
approchée (dite semence), imaginée a0 |
||
|
Formule de Héron |
|
|
|
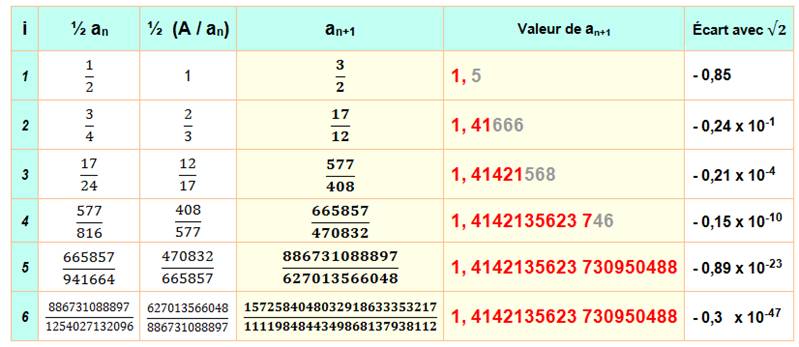
Exemples
On a pris A = 2.
Les fractions successives sont les réduites
obtenus à partir de la fraction continue de la racine. Notez l'extrême
rapidité de la convergence (10 décimales en 4 itérations). La
quantité de décimales exactes est doublée à chaque itération (convergence
quadratique)
Note
personnelle Vers 1970, j'ai eu à programmer cette
méthode en assembleur pour calculer une racine carrée intervenant dans une équation
radar. Le calculateur spécialisé que nous avions conçu comportait une
fonction addition et une fonction multiplication en dur (en circuits
électroniques). |
||
Voir Héron
et ses contemporains / Héron
= cas particulier de Newton
|
|
||
|
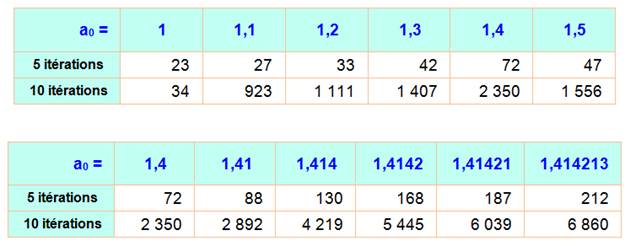
Convergence
selon la valeur de la semence
On donne l'écart en puissance de 10. Exemple avec A = 1,4 et 10 itérations, l'écart est 10 -2350 |
||
|
Choix
de la semence La
valeur la plus efficace et qui se calcule facilement est la racine du carré parfait
le plus proche du nombre dont on veut calculer la racine. Exemple: pour calculer la
racine de 98, on prendra 10 car 10² = 100. La troisième itération produira
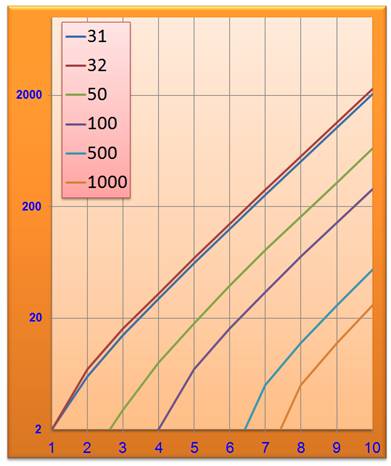
déjà 17 décimales. Illustration: Il s'agit du
calcul de la racine de 1000. En abscisse, la quantité d'itérations et en
ordonnées, la quantité de décimales exactes obtenues. La
courbe en bas à droite correspond à a0 = 1000. Les deux courbes en
haut à gauche correspondent à a0 31 et 32. Évidemment, plus la
valeur initiale se rapproche de la racine et plus la convergence est rapide.
Avec 31 ou 32 et dix itérations la racine est connue avec plus de 2000
décimales. Reste
qu'il faut faire les calculs! |
|
|
|
|
||
|
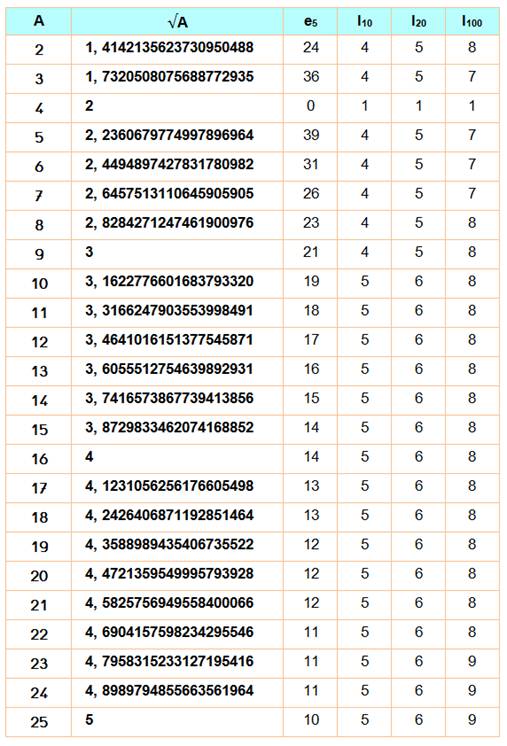
On
calcule l'écart après 5 itérations: E = 10-e |
On donne
e5 |
|
|
On
calcule le nombre d'itérations Ii pour
obtenir un écart inférieur à 10-i |
On donne I10 , 210
, I100 |
|
|
a0 = A/2
Conclusion Pour
les petits nombres, même sans estimation de la racine (a = A/2), avec 5
itérations, on obtient au moins 10 décimales. Ce qui suffit pour bon nombre
d'applications. |
||
|
|
||
|
Justification
algébrique |
|
|
|
|
A = a² + h |
|
|
|
a² + h + … = (a + …)² |
|
|
|
a² + h + h²/4a² = (a + h/2a)² |
|
|
|
a² + h |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Voir Algorithme de Newton |
||
|
Utilisation de la méthode de Newton pour la recherche
des racines. Elle consiste à s'approcher de la courbe par marches
d'escalier jusqu'à atteindre la racine sur l'axe des x (valeur de y pour x =
0). Illustr On dessine les courbes y = x² – A dont la valeur est A
pour x = 0 et la courbe des valeurs calculées y' = r² – A. |
(Échelle
non respectée) |
|
|
On donne les deux valeurs de y et y' au cours des itérations |
|
|
|
Question Trouvez
n minimum tel que Solution Multiplions
par le conjugué et calcul avec identité
remarquable:
En
reprenant l'inégalité:
Racine
de n est plus grand que racine de n – 1, mais les
deux sont proches: En
prenant le carré: Finalement
la valeur de n: En
effet: Mais: |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()