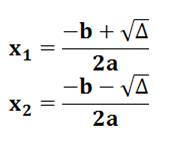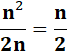|
|||||||||||||||||||||||||||||||||||||
![]()
|
ÉQUATIONS du 2e degré Somme & Produit Trouvez
deux nombres dont on connait la somme et le produit de deux nombres ? |
Voir Somme et produit
|
Problème de Viète: nombres dont on connait le produit et la
différence Trouver
les dimensions du rectangle dont l'aire vaut 20 et la différence entre côté
est 8. Viète (1591 – Nouvelle algèbre –
Zététiques III du livre I) |
|
Quels
sont les couples de nombres entiers x et y tels que:
|
|
2 + 2 = 4 2 x 2 = 4 11 + 1,1 = 12,1 11 x 1,1 = 12,1 |
|
|
la
somme et le produit des racines |
|
|
|
ax²
+ bx + c = 0 |
||
|
|
||
|
|
||
|
|
S = x1
+ x2 = –b/2a – = –b / a |
|
|
|
P = x1
. x2 = (–b/2a – = (–b/2a)² – ( = b²/4a² – = b²/4a² – b²/4a² + 4ac/4a² = c / a |
|
|
|
x² + bx/a + c/a = 0 |
|
|
x²
– Sx + P = 0 |
||
|
|
a + b =
7 & a . b = 10 est
solution de x² – 7x + 10 = 0 |
|
|
Solution des
équations en général ? |
||
|
Résolution des équations, relations
entre racines En 1832, Évariste Galois
montre qu'il est IMpossible de résoudre des équations
supérieures au quatrième degré. En revanche, il est possible de caractériser les relations entres les racines et de mettre en
évidence leurs symétries. Par exemple x² – 2 =
0 a deux racines symétriques: |
Exemple avec une
équation du second degré dont les racines sont r et s: À comparer à: La constante c vaut le
produit des racines et le coefficient b de x, la somme des racines. |
|
|
Il existe un outil ingénieux qui permet de progresser
sur la connaissance des racines des équations: les nombres p-adiques. On démontre que, s'il existe une solution dans ce
monde p-adique, alors la solution existe aussi en réel. |
||
Merci à JL Barre pour sa relecture attentive
![]()
|
SOMME ET PRODUIT –
Recherchons les
racines de cette nouvelle équation |
|
|
|
|
x²
– Sx + P = 0 |
|
|
|
x1 = s + x2 = s – |
|
|
|
x1
= s + t x2
= s – t |
|
|
|
x1
+ x2 = 2s = S |
|
|
|
x1 . x2 =
s² – (s² – P) = P |
|
|
SOMME ET PRODUIT – Exemple |
|
|
|
|
S = a + b = 7 P = a . b = 10 |
|
|
|
x²
– 7x + 10 = 0 |
|
|
|
S²
– P = (7/2)² – 10 = 49/4 – 40/4 = 9/4 |
|
|
|
|
|
|
|
x1
= S + x2
= S – |
|
Voir Trouver k nombres
connaissant la somme et le produit
|
SOMME ET PRODUIT – Exemple de
raisonnement avec imaginaires |
|
|
|
|
S
= 2 (soit s = 1) P
= 4 |
|
|
|
x²
– Sx + P = 0 x²
– 2x + 4 = 0 |
|
|
|
x1
= s + t = 1 + t x2
= s – t = 1 – t |
|
|
|
x1
. x2 = (1 – t)(1 + t) = 1 – t² |
|
|
|
P
= 4 |
|
|
|
1
– t² = 4 t²
= -3 |
|
|
|
t² = 3i² t1 = i t2
= – i |
|
|
|
x1 = 1 + i x2 = 1 – I |
|
|
|
x1
+ x2 = 2 |
|
|
|
x1 . x2 =
1 – 3i² = 1 + 3 = 4 |
|
|
|
||
Suite en Somme des inverses et généralisation
somme et produit
|
|
||
|
Somme et produit dans l'équation du deuxième degré |
Surface = produit, alors que Périmètre = double de la somme |
|
|
Alors attention à cette autre notation
impliquant un facteur 2 Si
S* = Surface (qui est un produit) et, P* = Périmètre (qui est une somme). La
formule devient: x.y = P = S* 2 (x + y) = 2S = P* x² – P*x / 2 + S* = 0 |
||
Voir Problème
babylonien
|
Problème de Viète: nombres dont on connait le produit et la
différence Trouver
les dimensions du rectangle dont l'aire vaut 20 et la différence entre côté
est 8. La
solution est basée sur cette identité
remarquable:
Il
suffit d'y reporter nos nombres: (8)² + 4 x 20 = 144 = 12² = (a +
b)² La
somme est 12 et la différence 8 (a + b) + (a – b) = 12 + 8 = 20 =
2a a = 10 et b = 2 Autre exemple Produit = 12 différence = 1 1² + 4 x 12 = 49 = 7² => a = 4
et b = 3 |
Retour / Carré et carrés inférieurs
(propriété générale)
Autre devinette
|
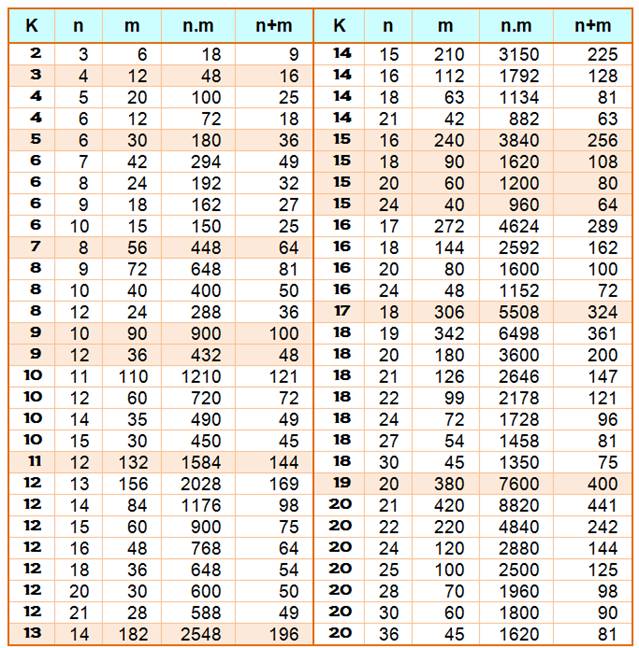
Quels sont les trois couples
de nombres entiers x et y tels que le
produit divisé par la somme = K. Toutes les réponses
données à droite sont les seules possibles. Évidemment, il existe
toujours une solution du type:
Par contre, pour
trouver les autres, ce n'est pas évident par calcul. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table des couples (n et m) pour K de 2 à 20
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()