|
Édition du: 25/09/2022 |
|
INDEX |
Le petit théorème de Fermat |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Collier de perles pour aborder le petit théorème de
Fermat Quelle
idée ! Expliquer le petit de théorème de Fermat, un théorème de la théorie
des nombres, en comptant des colliers de perles … Cette
manière de voir est due à une idée de Julius Petersen (1872) concrétisée par
Solomon Golomb (1956). |
||
|
|
Sommaire de cette page >>> Compter les colliers de couleur >>> Petit théorème de Fermat |
Débutants Glossaire |
|
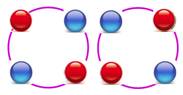
Cas où p est premier Prenons ce collier formé de cinq perles de trois couleurs. p = 5 et a = 3 Combien pouvons-nous former de colliers
différents? Pour chaque perle, il y a trois choix: Les trois colliers d'une seule couleur sont
exclus. Les rotations ne sont pas admises.
Remarque importante Ce nombre Q est un
entier puisqu'il est le résultat d'un dénombrement. Ce qui veut dire que (ap – a) est divisible par p. |
Collier 5-3
Trois colliers d'une seule couleur
Cinq colliers identiques par
rotation de 72°
|
|
|
Cas où p est composé Prenons ce collier formé de quatre perles de
trois couleurs. p = 4 et a = 3 La quantité de colliers identiques par rotation
n'est pas 4, mais 2. On ne peut plus diviser par p. Conséquence: pour respecter notre formule en Q,
le nombre p doit être
premier. |
Collier 4-3
Deux colliers identiques par
rotation de 90°
|
|
|
Forme arithmétique On reprend le compte de colliers et on multiple
par p. Cette relation montre qu'un nombre (a) à la
puissance d'un nombre premier (p) diminué de sa propre valeur est un multiple
de ce nombre premier. |
Exemples
|
|
|
Forme mathématique On lit: a puissance p est congru à a modulo p Ce qui veut dire que ap et a divisés par p ont le même
reste. Ou encore que le reste de la division de ap par p est:
|
Exemple
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
Le petit théorème de Fermat
|
|
Voir |
|
|
Sites |
|
|
Cette page |