|
||||||||||||||||||||||||||||||||||||||||
![]()
|
PETIT THÉORÈME DE FERMAT Nous allons approcher par
l'expérience (et amusement) le Petit Théorème de
Fermat (PTF) relatif à la divisibilité des nombres. L'expérience est relativement
simple et très amusante. Instructive de surcroît ! Laissez-vous prendre
par la main… Vous aurez la satisfaction de comprendre un point important de
la théorie des nombres. Pour ceux qui ont
des notions sur le modulo, vous pouvez allez directement voir Modulo et Fermat. Impatient ! Tout
de suite, donnez-moi la formulation du théorème. D'un
coup d'œil
Exemple
|
|
C'est
ce genre de découverte qui fait bouillir les
sangs d'un mathématicien. Marcus du Sautoy – La symphonie des
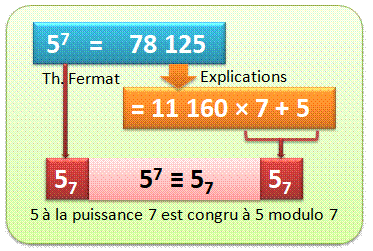
nombres premiers Cette formule se lit:
divisés par un nombre premier p un nombre et sa puissance p ont le même
reste. Exemple:
53 = 125, divisé par 3, reste 2
et 5 divisé par 3, reste 2. Sous forme de koan Zen
|
Voir
Citations de maths
/ Pensées & humour
|
|
||
|
Principe p étant un nombre
premier:
Un
nombre et sa puissance p, divisés
par p donnent le même
reste. |
Exemple Trouvez le reste de
la division de 87 par 7:
Il
suffit de donner le reste de la
division de 8 par 7, soit 1. En
effet 87 = 2 097152 = 299 593 x 7 + 1 |
|
|
Comme souvent en maths,
l'idée est de trouver des routes plus simples, moins fastidieuses. Ici on remplace la voie du bas, difficile à calculer, par celle du haut
qui donne un résultat immédiat. |
||
Voir
Magie
|
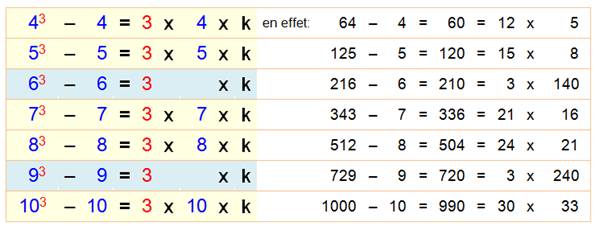
Toutes
ces configurations en puissance 3 sont divisibles par 3 (petit théorème de
Fermat) et certaines aussi par le nombre (bleu). Les exclus sont les
multiples de 3 (lignes de couleur bleu clair).
|
Voir Divisibilité
|
|
|||||||||||||||||||||||||||||
|
D'abord
Extraordinaire !
C'est
le constat que Fermat a dû faire. Mais
d'une curiosité, il en a tiré un théorème. Ce
pourrait être du style: Divisé par p,
un nombre et sa puissance p donnent le même reste. |
|||||||||||||||||||||||||||||
|
|
|||
|
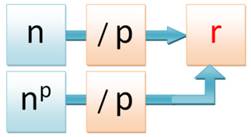
Modulo m |
Je
divise par m et ne
m'intéresse qu'au reste. |
15 mod 12 = 3 Pensez à 15 heures modulo 12 |
|
|
Résidu b |
Le
reste b de cette division. |
3 est le reste ou résidu. |
|
Voir explic
|
|
|||||||||||||||||||||||||||||||||
|
Procédons par étapes
Ét
de
tous les nombres a de 1 à 3.
Ét
|
|||||||||||||||||||||||||||||||||
|
Ét
En effet 4
/ 3 donne un reste de 1, et, en retranchant le reste. (4
– 1) / 3 donne un reste de 0. Voici le t
Ét
en
puissance n = 2, on a toujours 1 en
puissance n = 3, on a des chiffres qui tous valent a Ét
Étape 6 – Expressions littérales
Vrai dans
cet exemple! Est-ce toujours vrai? C'est ce que nous allons voir.
en
n = m – 1 , on a 1. en
n = m, on a des chiffres qui valent a.
Étape 7 - Théorème ? On peut déjà imaginer des propriétés générales. Avec diverses
formulations équivalentes
Nous
allons voir que ça n'est pas complètement exact. Ét |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
Tableau avec m = 4
Tous
les nombres internes au tableau sont divisible par 4 (= 0 mod 4).. Exemple: 32 – 1 = 9 – 1 = 8 et 8 est divisible par 4. Expressions littérales
Propriétés
Conclusion
Continuons notre exploration avec m = 5, qui est premier comme
3
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Tableau avec m = 5, ou plutôt p = 5, pour bien témoigner du
fait que 5 est premier
Expressions littérales
Propriétés
un
nombre à la puissance p moins ce nombre est divisible par p. a p – a
est divisible par p pour
tout p premier.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
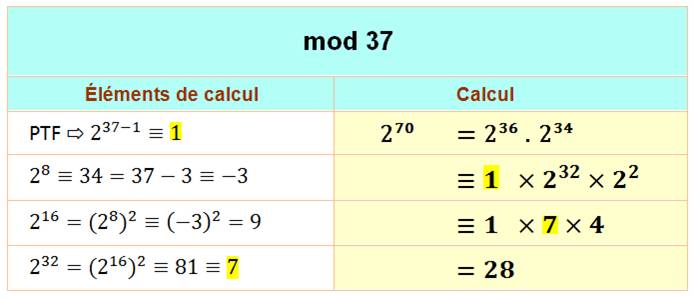
Tableau avec p = 7
Symboles
Remarque
Le pourquoi de ce nom de baptême Z7, sera vu
ultérieurement.
On
élimine la ligne 1 (puissance 1), et on ne note plus que les résidus.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||
|
Formulations classiques (à retenir) du petit théorème de
Fermat
(a,p) = PGCD
et (a,p) = 1 indiquent que a et b sont étrangers
(premiers entre eux) Autres formulations
Quelques exemples pour bien se remettre en tête cette
extraordinaire propriété: 22
– 1 = 0 mod 3 32
– 1 42
– 1 = 0 mod 3 52
– 1 = 0 mod 3 62
– 1 Tous les carrés sont de la forme 3k + 1 sauf pour
les nombres divisibles par 3. |
|||||||||||
|
|
|
|
|
|
Voir Calculs du
même style / Algorithme de calcul modulaire
|
|
|
|
|
|
|
|
|
|
Fermat's Little Theorem:
|
|
![]()
|
Le petit théorème de Fermat
|
|
|
Voir |
|
|
Avancé |
Voir
un sujet complet utilisant ces notions: On y
verra en particulier le cas de la puissance 15 |
|
Découvrir |
|
|
Cette page |
![]()