NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/03/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Carrés magiques
Débutants Carrés magiques	Rectangles magiques				Glossaire Carrés magiques
INDEX Carrés magiques Jeux	Rectangles		Rectangles pairs	Rectangles impairs
	Rectangles 3 x 5		Rectangle de Kotzig	Rectangles premiers
	Pavé magique		Rectangle à répétitions
		Sommaire de cette page >>> Rectangles magiques impairs – Exemples

Rectangles magiques 3 x 5

Étude et exemples

Le plus petit rectangle magique. Sans la contrainte sur les diagonales, évidemment les rectangles magiques, même pour le plus petit, sont extrêmement nombreux.

Rectangles magiques impairs – Exemples
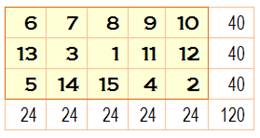
Rectangle 3x5 Données magiques m = 5, n = 3 N de 1 à 3x5 = 15 S = ½ 15 x 16 = 120 M = ½ (3 x 5 + 1) = 8 SL = 5 x 8 = 40 SC = 3 x 8 = 24 Constante associative 9+7 = 11+5 = 12+4 = 6+10 = 2 +14 = 16 = c 5c = 2 x 40 c = 16 Le calcul littéral donne c = nm + 1 Voir Données magiques	Rectangle 3x5 normal puis normal et associatif Autre exemple normal avec 1 central

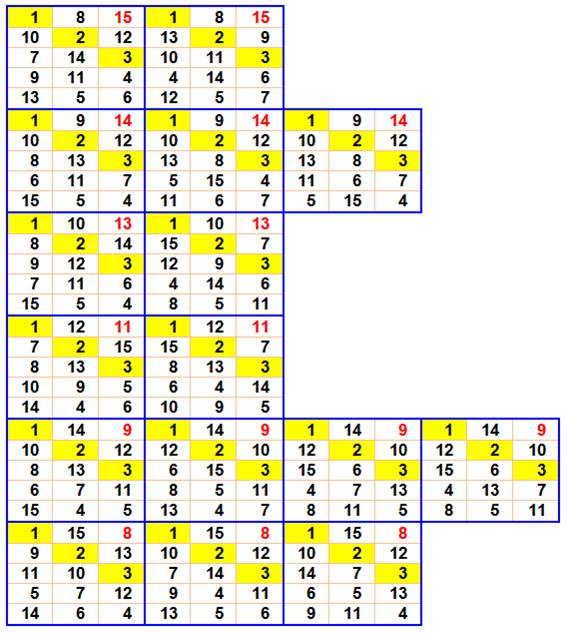
RM 3 x 5 avec contrainte 123
Les 16 configurations possibles (hors les permutations entre lignes et colonnes). La position des nombres 1, 2 et 3 est imposée. Chaque ligne de carrés associe le 1 initial aux nombres maximums successifs possibles: 15, 14, 13 … Avec le 1 dans cette position, aucun n'est associatif. L'idée sous-jacente: le 1 et 2 sur la même ligne est impossible, car il faudrait 21 pour atteindre 24, nombre supérieur à15. première configuration possible: 1 + 15 + 8 = 24

Retour	Rectangles magiques
Suite	Rectangle de Kotzig Pavé magique Carrés magiques – Index
Voir	Tous les carrés plus que parfaits 4x4 Carré plus que parfait 8x8 Carrés magiques – Index Jeux – Index
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaCMag/RecMag35.htm