|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Rectangles magiques Moins
connus que les carrés magiques, le rectangle magique présente
quelques intérêts en combinatoire.
Notamment, est-il possible de construire n'importe quel rectangle magique
d'ordre m.n. Avec eux,
la constante magique est la moyenne magique,
identique sur chaque ligne et chaque colonne, et elle vaut M = (m.n + 1) / 2. De sorte que la somme en ligne
est égale à m.M et la somme en colonne vaut n.M. Ce sont les deux constantes
magiques. Les
rectangles sont semi-magiques avec deux
constantes. |
Anglais: Magic rectangle
|
|
||
|
Définition Un
rectangle est magique si les sommes sur les lignes sont égales et les sommes
sur les colonnes le sont aussi. Ou: si la moyenne
des nombres sur chaque ligne et chaque colonne est constante. Le
rectangle magique est normal si les
nombres de la grille vont de 1 à m.n. Il est associatif si les sommes des deux nombres
opposés à la périphérie sont égales. Questions Pourquoi
pas une seule somme magique? La réponse est donnée par le calcul ci-contre
montrant comment calculer la somme totale dans le rectangle et les deux
sommes magiques. Et les
diagonales? À l'évidence, impossible de définir les diagonales. |
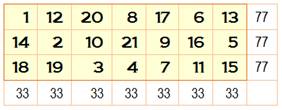
Exemple de rectangle 3 x 7
Ce rectangle est normal (nombres de
1 à 21). Présentation avec le nombre 1 dans le coin
haut-gauche.
Celui-ci est normal et associatif (10 + 12 = 22 …). La somme de tous les nombres étant 1 + 2 + 3 + … + 21 = ½ x 21 x
22 = 231, la somme des lignes est 231/3 = 77 et celle sur les colonnes est: 231/7 = 33 Voir Somme des entiers Moyenne magique Moyenne ligne: 77 /
7 = 11 Moyenne colonne: 33 / 3
= 11 Moyenne magique: 231 / (3x7) = 11 |
|
|
|
||
|
Le plus
petit rectangle magique. Dimension: 2 x 3 Nombres: de – 3 = + 3 L'utilisation
des nombres négatifs n'est pas l'usage et, de plus, sans beaucoup d'intérêt. Les sommes comme la moyenne sont nulles. Par contre
le carré du bas utilise des nombres positifs mais n'est pas normal. La moyenne magique est: 12/ 3 = 4 et 8/2 = 4. Comme les
diagonales n'interviennent pas, les lignes et colonnes peuvent être permutées
à loisir. Il plus simple de donner un des représentants en plaçant le 1 en
haut à gauche. |
Rectangle 2 x 3
Rectangle générique 2 x 3
Rectangle 2 x 3 positif
Ce rectangle est le représentant de 12 autres obtenus par
permutations. Nombres utilisés: de 1 à 7, avec la 4 exclu. |
|
|
Rectangle 2 x 3 normal Il
n'existe aucun rectangle 2 x 3 normal. |
Somme des nombres de 1 à 6: ½ x 6 x 7 = 21 Moyenne ligne: 11 / 2 = 5,5 Moyenne colonne: 11 / 3 = 3,66… Pas compatible avec un rectangle normal 2 x 3. |
|
|
|
||
|
Ils sont
48 obtenus par permutations de celui présentée ci-contre. Pour le composer, on calcule les paramètres (ou, on les lit dans le
tableau ci-dessus) S = 36, SL = 18, SC = 9. M = 4,5 On place immédiatement le 1 et 8 en colonne de gauche. Les couples de somme 9 sont (2, 7), (3,6) et (4,5). Seul triplet sommant en 10: (2,
3, 5), nombres qu'il suffit de placer sur la ligne du bas. |
Rectangle 2 x 4 normal
Ce rectangle est le représentant de 48 autres obtenus par permutations
(isomorphisme). Il est le
plus petit rectangle normal. Principe de construction
|
|
|
et existence des rectangles normaux |
|
|
|
Tableau Toutes
les possibilités pour m et n jusqu'à 15 pour lesquelles les sommes sur les
lignes ou les colonnes sont des valeurs entières. Ex: 3 x 7 vu ci-dessus. Ce qui
veut dire que pour toutes les autres possibilités, il n'existe pas de
rectangle magique. Ex: 2x3 ou 2x5, etc. Données magiques d'un rectangle n . m Nombres
utilisés: de 1 à m.n Somme
totale
Somme
ligne
Somme colonne
Moyenne
magique
Remarquez
que m et n sont toujours de même parité. Théorème prouvé par Hamuth en 1881. Thomas Hagedom a proposé une
méthode de construction. |
Légende: L =
quantité de lignes; C = quantité de colonnes; S = somme totale; SL = somme
sur chaque ligne; SC = somme sur chaque colonne.
Selon la parité de chacun
m et n doivent
être même parité. Pas de rectangle
magique avec m et n de parités différents. Remarque Ce tableau donne la condition nécessaire pour l'existence
d'un rectangle magique. Mais est-elle suffisante? |
|
|
Théorèmes sur l'existence des
rectangles magiques (RM) Un rectangle magique RM(a,b) existe si et seulement si a, b > 1, a.b > 4 et a Divers auteurs dont Rivora, Trenkler, Pebody … Voir Référence |
Pas de RM si dimensions m et n sont de parités
opposées. Les RM 3x5, 3x7, 5x7 existent >>> Il existe des algorithmes relativement simples
pour:
|
|
|
|
||
|
Magic rectangle Normal rectangle Associated rectangle Row, column |
A magic rectangle is a rectangle array of
numbers whose row totals are all the same. as well as the column totals. Magic rectangles are well-known for their
very interesting and entertaining combinatorics. In a magic rectangle, the
integers 1 to mn are arranged in an array of m rows and n columns so that
each row adds to the same total M and each column to the same total N. (…) therefore, an odd by even magic
rectangle is not possible. |
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaCMag/RecMag.htm
|
![]()