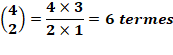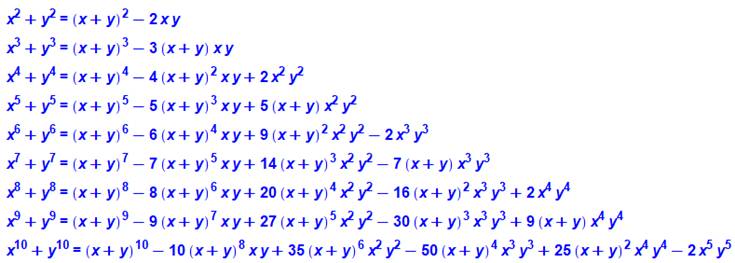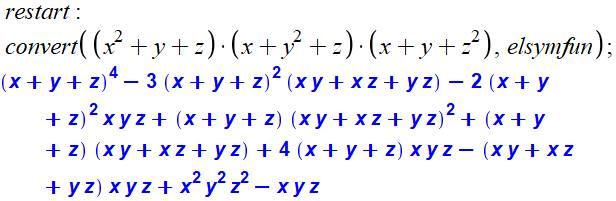|
Édition du: 10/09/2023 |
|
INDEX |
Polynômes |
||
|
(Girard-Newton) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Polynômes symétriques Polynômes ou fonctions symétriques
élémentaires (PSE ou FSE) Polynôme
invariant par permutations des variables. x² + y² est symétrique, mais pas x²
+ y. Ils sont élémentaires si du premier degré comme x + y + z ou xyz ou
encore xy + xz + yz. Les polynômes
symétriques jouent un rôle important dans l’étude des racines des polynômes. Théorème
fondamental des fonctions symétriques (simplifié): Tout polynôme symétrique s'exprime de façon unique par une combinaison
de polynômes symétriques élémentaires. |
||
|
|
Sommaire de cette page >>> Approche >>> Théorème fondamental des fonctions
symétriques >>> Polynômes symétriques élémentaires >>> FSE des racines >>> Programme |
Technique de base de l'algèbre |
Anglais: Symmetrical
polynomial
|
Polynôme symétrique Un polynôme symétrique reste invariant en
inversant (commutant) ses variables. Parmi les polynômes symétriques on trouve:
|
Exemples avec trois variables X + Y + Z XY + YZ + ZX XYZ X² + Y² + Z² X3YZ + XY3Z + XYZ3 |
|
|
Polynôme symétrique élémentaire Ce sont tous les polynômes possibles du premier
degré. Ces polynômes engendrent l'algèbre (commutative)
des polynômes symétriques |
Exemples avec trois variables X + Y + Z XY + YZ + ZX XYZ |
|
Voir Tous
les types de polynômes / Brève
52-1039
|
Cas
d'une variable |
P1
= X1 (Utilisation des grands X pour plus de clarté avec les indices) |
|
|
Cas
de deux variables |
P1
= X1 + X2 P2
= X1X2 |
|
|
Cas
de trois variables |
P1
= X1 + X2 + X3 P2
= X1X2 + X1X3 + X2X3
P3
= X1X2X3 |
|
|
Cas
de quatre variables |
P1
= X1 + X2 + X3 + X4 P2
= X1X2 + X1X3 + X1X4
+ X2X3 + X2X4 + X3X4 P3
= X1X2X3 + X1X2X4
+ X1X3X4 + X2X3X4
P4
= X1X2X3X4 |
|
|
Cas
de n variables
Notation Ces polynômes
sont souvent notés:
Quantité
de termes dans P C'est la combinaison
de p possibilités parmi n. Exemple avec P2
pour quatre variables:
|
||
|
Relation avec les équations Un polynôme du second degré peut s'écrire de deux
manières:
Polynômes symétriques P1
et P2 Les racines (lambda) sont liées par des relations
symétriques: chaque racine joue le même rôle. C'est le cas quel que soit le degré du polynôme. Cas du troisième degré Un polynôme du troisième degré peut s'écrire de
deux manières:
Cas général de degré n Un polynôme de degré n peut s'écrire de deux
manières:
|
Fonctions symétriques élémentaires des racines
|
|
|
Théorème fondamental des fonctions
symétriques Soit un polynôme symétrique à n variables, alors
il existe une unique fonction polynomiale
combinant ses n fonctions symétriques élémentaires.
|
Exemple Tout polynôme symétrique à trois variables peut
s'écrire comme combinaison des trois polynômes élémentaires indiqués
ci-dessus. |
|
Décomposition de polynômes symétriques en
polynômes symétriques élémentaires
|
Sommes de Newton (somme de
puissances) et leur décomposition en polynômes symétriques élémentaires
(celles-ci sont uniques). Deux variables
Trois variables
|
Voir Application à la résolution
d'une énigme
|
Quelques autres décompositions en
polynômes symétriques élémentaires
Note: du fait de la commutativité, quelques unes de ces
expressions sont redondantes. |
|
Instruction Maple réalisation la décomposition polynôme
symétrique en polynômes symétriques élémentaires
Programme pour copier-coller dans Maple restart;
convert((x^2+y+z)*(y^2+x+z)*(z^2+x+y), elsymfun) |
Voir Programmation – Index
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Sites |
|
|
Cette page |