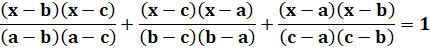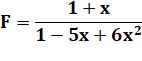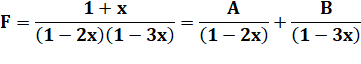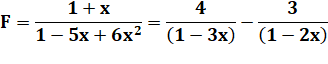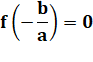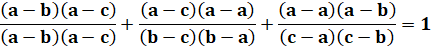|
||||||||||||||||||||||||||||||||
![]()
|
Propriétés des polynômes Les principaux théorèmes caractérisant les polynômes, leurs racines et leurs
factorisations.
|

|
Prouvez cette
identité:
|
|
|
|||
|
Il est
des cas où il est intéressant de décomposer une fraction
polynomiale en somme de fractions. Ici, il
s'agit de trouver deux fractions avec de polynômes du premier degré.
Autrement-dit: transformer le deuxième degré en premier degré. |
|
||
|
Factoriser
le dénominateur. |
1
– 5x + 6x² = (1 + ax)(1 + bx) = 1 + (a + b)x + abx² ab = 6 et a + b = – 5 => a = –2 et b =
–3 |
||
|
Avec la
somme des deux fractions cherchées, la fraction devient: |
|
||
|
En
réduisant les deux termes de la somme au même
dénominateur, le numérateur devient: |
1
+ x = A(1 – 3x) + B(1 – 2x) =
A + B – x(3A + 2B) A
+ B = 1 et 3A + 2B = - 1 B
= 1 – A => 3A + 2(1- A) = -1 =>
A = -3 B
= 1 + 3 = 4 |
||
|
Finalement |
|
||
|
|
||
|
Soit le polynôme
Si an et a0
sont des entiers non nuls, et si une fraction irréductible p/q est racine du
polynôme, alors p divise a0 et q divise an. On déduit
que si an est égal à 1 (polynôme
unitaire), alors la racine est
un nombre entier, un des diviseurs de a0. Attention
au signe. Voir
Irrationnalité |
EXEMPLE 1
Selon le théorème
Essais
La racine réelle est 2 et la
factorisation donne :
EXEMPLE 2
Pour x = 1, le polynôme en x dépasse 14 : la racine réelle est
inférieure à 1 Selon le théorème
Essais
La racine réelle est 2/3 et la
factorisation donne :
|
|
Anglais
Rational Root Theorem
|
|
|||||
|
On rappelle
qu'il est parfois possible de factoriser un polynôme du second degré à la
simple lecture des coefficients. |
P = x² + 3x + 2 2 est le produit des racines: 1 et 2 ? 3 est
l'opposé de la somme des racines: –1 et –2 P = (x + 1) (x + 2) |
||||
|
Exemples avec déclinaison des signes |
|||||
|
x² + 3x + 2 x² – x – 2 x² + x – 2 x² – 3x + 2 |
P = +2 et S = –3 P = –2 et S = +1 P = –2 et S = –1 P = +2 et S = +3 |
x1 = –1 & x2 = –2 x1 = –1 & x2 = +2 x1 = +1 & x2 = –2 x1 = +1 & x2 = +2 |
=> (x + 1) (x + 2) => (x + 1) (x – 2) => (x – 1) (x + 2) => (x – 1) (x – 2) |
||
|
x² + 9x + 14 x² – 5x – 14 x² + 5x – 14 x² – 9x + 14 |
P = +14 et S = –9 P = –14 et S = +5 P = –14 et S = –5 P = +14 et S = +9 |
x1 = –2 & x2 = –7 x1 = –2 & x2 = +7 x1 = +2 & x2 = –7 x1 = +2 & x2 = +7 |
=> (x + 2) (x + 7) => (x + 2) (x – 7) => (x – 2) (x + 7) => (x – 2) (x – 7) |
||
|
Exemples moins évidents |
|||||
|
x² + 5x – 104 |
P = –104 et S = –5 104 = 2 x 52 = 4 x 26 = 8 x 13 |
x1 = +8 & x2 = –13 |
=> (x – 8) (x + 13) |
||
|
2x² + 5x – 3 = 2(x² + 5/2 x – 3/2) |
P = –3/2 et S = –5/2 |
x1 = +1/2 & x2 = –3 |
=> 2 (x – 1/2) (x + 3) = (2x – 1) (x + 3) |
||
|
|
||
|
Théorème du reste polynomial ou petit théorème de Bézout: |
Le reste d'une division d'un polynôme f(x) par
x – a est égal à f(a). ssi: si et seulement si |
|
|
Exemple |
Division de f(x) = 2x6 – 5x3
+ 1 par x + 2. Le reste de la division est égal à f(a) avec a =
–2. Soit: f(a) = 2(–2)6 – 5(–2)3 + 1 = 2 x
64 – 5 x (–8) + 1 = 128
+ 40 + 1 = 169 = 13² |
|
|
Démonstration |
|
|
Anglais: Remainder
theorem
|
|
||
|
Théorème de factorisation des polynômes |
Si (x – a) est un facteur du
polynôme f(x), alors f(a) = 0. Réciproquement si f(a) = 0,
alors (x – a) divise f(x). |
|
|
Exemple 1 |
En prenant x6 – 1, une racine évidente
est 1 car f(1) = 16 – 1 = 0 Ce qui veut dire que x6 – 1 est divisible par (x + 1). On dit aussi: (x + 1) est facteur de x6 – 1.
|
|
|
Exemple 2 |
On sait que 7 est racine de x4 – 2x3 – 32x2 – 19x – 14, factorisez ce polynôme.
= (x – 7) (1x3 + bx2 + cx + 2) Développement de cette expression = x4 + (b–7)x3 + (–7b +c)x2 + (–7c+2) – 14 Soit le jeu d'équations en rapprochant du
polynôme initial: b – 7 = –2 –7b + c = –32 –7c + 2 = –19 Bilan: x4 – 2x3 – 32x2 – 19x – 14 = (x – 7)
(x3 + 5x2 + 3x + 2) |
|
|
Démonstration |
|
|
Anglais: Factor
theorem
|
|
||
|
Racine double |
Si a est racine double de f(x), alors f(x) est
divisible pr la carré de (x – a): f(x) ) = (x – a) (x – a )
g(x) = (x – a)² g(x) |
|
|
Généralisation |
Si (ax + b) est facteur de f(x), alors:
Exemple (3x + 2)
(x² + x + 1) = 3x3 +5x² +
5x + 2 f
(-2/3) = 0 |
|
|
Plusieurs diviseurs |
Si (x + a) La barre verticale veut dire: divise Autrement dit: Si (x+a)
et (x+b) divisent f(x) alors:
Exemple x4 – 10x3 + 35x2
– 50x + 24 = (x – 1) (x – 2) (x2
– 7x + 12) = (x – 1) (x – 2) (x – 3) (x –
4) f(1) = f(2) = f(3) = f(4) = 0 Pour l'amusement (x – a) (x – b) (x – c) (x – d) = x4 – (a + b + c + d)x3 + (ab + ac + ad + bd + bc + cd)x2 – (abc + abd + acd + bcd)x + abcd f(a) = f(b) = f(c) = f(d) = 0 |
|
Le
coin de l'expert – Définitions
|
Soit un corps
K commutatif comme celui des nombres réels
R. Un polynôme P à coefficients dans K est une suite
an (n entier) indexée sur N d'éléments de K tous nuls sauf un
nombre fini (ce sont les coefficients de
P). On note:
Si P n'est pas nul, son degré est
le plus grand entier d tel que ad est différent de 0. On convient
que deg(0) = – ∞ (moins l'infini). Un monôme est un polynôme dont au
plus un des coefficients est non nul. Un polynôme est unitaire (monic en anglais) si son coefficient de plus haut degré
est égal à 1. La somme, la différence, le produit de deux polynômes, le produit d'un
polynôme par un élément de K ont un sens naturel et possèdent les propriétés
de commutativité, associativité, distributivité … pour que l'ensemble K[X]
des polynômes soit muni d'une structure
d'anneau, de K-espace vectoriel et de K-algèbre. La composition de deux polynômes a également un sens et n'est pas
commutative. |
Suite Polynômes – Exo 7 ou Polynômes et fractions rationnelles – Université de Lyon
|
Prouvez cette identité:
Avec x = a, on a:
x = a est une racine de
l'équation. On montrait que x = b et x = c sont également racines. On a donc trois racines (a, b et
c). On ne s'arrête pas là! En effet,
l'équation est du deuxième degré et ne
possède pas plus de deux racines. Avec trois, une de superflue,
l'équation est valable pour toute valeur de x et c'est une identité. |
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()