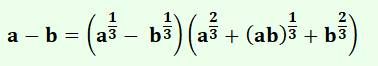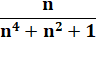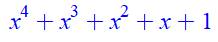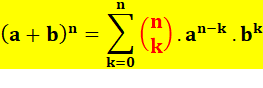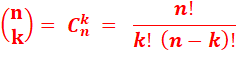NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Algèbre
Débutants Algèbre	IDENTITÉS			Glossaire Algèbre
INDEX Identités Algèbre	Remarquables	Degré > 2	Spéciales	Divers
	Inverses	a^n – b^n (moins)	a^n – 1	Complexes
	Puissances	a^n + b^n (plus)	(x+ x² + …) ^k	Trigonométrie
	Newton	Puissance 5	Héron	Moivre
	Dévelop. limités	Euler & Riemann	Racines (degré 1/n)	(a + b + c + d)^k
	Ramanujan	Degré 7	Polynômes symétriques élémentaires
		Sommaire de cette page >>> Identités degré 3 >>> Identités degré 4 >>> Identités degré 5 >>> Identités degré n >>> Identités en nk – n avec k impair >>> Binôme de Newton >>> Table des développements de (a – b)^n et (a + b)^n >>> Identités en a^n et b^n >>> Division (x^a – y^a) / (x^b – y^b)

IDENTITÉS REMARQUABLES

& Formules à noter

de degré supérieur à 2

Identités remarquables en puissance n

Voir Développements, notamment usage en numération

Vocabulaire: on parle d'identités ou de formules remarquables ou … moins remarquables.

Développement "magique" avec les coefficients polynomiaux

Pour développer (a + b)ⁿ ou (a + b + c + …)ⁿ , etc. , utilisez le calcul des coefficients multinomiaux. Une simple fraction de factorielles.

Exemple: pour (a + b + c)⁶

Formules de degré 3 et plus

IDENTITÉS avec le 3^e degré
(a + b)^3	=	a^3 + 3a²b + 3ab² + b^3 >>>
(a – b)^3	=	a^3 – 3a²b + 3ab² – b^3
a^3 – b^3	=	(a – b) (a² + ab + b² ) >>>
a^3 – 1	=	(a – 1) (a² + a + 1 )
a^3 + b^3	=	(a + b) (a² – ab + b² ) Somme de deux cubes divisible par somme des nombres. Ex: 9^3 + 9^3 = 18 x 81.
a^3 + c^3 Quelle que soit la valeur de b	= =	(a – b) (a² + ab + b² ) + (c + b) (c² – cb + b² ) (a^3 – b^3) + (c^3 + b^3)
a^3 + b^3 + c^3 – 3abc	=	(a + b + c) (a² + b² + c² – ab – bc – ca) Identité de Gauss >>>
a^3 + b^3 + c^3	=	3abc lorsque (a + b + c) = 0 >>>
a^3 + 2b^3 + c^3	=	(a + b) (a² – ab + b² ) + (c + b) (c² – cb + b² )
a^3 + 1	=	(a + 1) (a² – a + 1 )

(a² + 1) (a + 1)	=	a^3 + a² + a + 1
(a² + 1) (a – 1)	=	a^3 – a² + a – 1
(a² – 1) (a + 1)	=	a^3 + a² – a – 1
(a² – 1) (a – 1)	=	a^3 – a² – a + 1
(a + 1)² (a + 1)	=	a^3 + 3a² + 3a + 1
(a – 1)² (a – 1)	=	a^3 – 3a² + 3a – 1
(a + 1)² (a – 1)²	=	a^4 – 2a² + 1

Merci à Roger Rainero

(a^2 + a – 1) (a + 1)	=	a^3 + 2a^2 – 1
(a^2 – a – 1) (a – 1)	=	a^3 – 2a^2 + 1
(a + b + c)^3	=	a^3 + b^3 +c^3 + 3 ( a²b + a²c + b²c + ab² + ac² + bc² ) + 6 abc
(a + b)^3 + (a – b)^3	=	2a^3 + 6ab²
(a + b)^3 – (a – b)^3	=	2b^3 + 6a²b
(a + b)^3 * (a – b)^3	=	a^6 – 3a^4b^2 + 3a^2b^4 – b^6
(a + b)^3 / (a – b)^3		rien d'intéressant
(a–b)^3 + (b–c)^3 + (c–a)^3	=	3(a – b)(b – c)(c – a)

n^3 – n	=	(n – 1) n (n + 1) >>>
n^3 + (n + 1)^3	=	(2n + 1) (n^2 + 2n + 1) >>>
(n + 1)^3 – n^3	=	3n² + 3n + 1 >>>
n^3 – (n – 1)^3	=	3n (n – 1) + 1 >>>
(n + 1)^3 + (n – 1)^3	=	2n^3 + 6n
(n + 1)^3 – (n – 1)^3	=	6n² + 2
(n + 1)^3 + n^3 – (n – 1)^3 – (n – 2)^3	=	12n (n – 1 ) + 10 >>>
(n² + 3n + 1)^2	=	n (n + 1) (n + 2) (n + 3) + 1 >>>

Suite: Somme de cinq nombres à la puissance p

Voir Somme de cubes et nombres d'Eisenstein / Nombres de dizaines et unités /

Applications (élimination de la racine cubique au dénominateur)

Racines cubiques

Voir Calculs avec les racines cubiques

Puissances et factorielles

La énième différence finie des puissances énièmes

est égale à factorielle n.

Voir Explications et démonstration

Identité de Bachet

Ex: 8³ – 2² = 2 288³ – 109 442² = 508

Voir Équation de Bachet

Identité de Fermat

Voir Application

Identité de Viète

Identité de Ramanujan

(3a² + 5ab – 5b²)³ + (4a² – 4ab + 6b²)³ + (5a² – 5ab – 3b²)³

= (6a² – 4ab + 4b²)³

= 8 (3a² – 2ab + 2b²)³

IDENTITÉS avec le 4^e degré
a^4	=		>>>
(a + b)^4	=	a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4
(a – b)^4	=	a^4 – 4a^3b + 6a^2b^2 – 4ab^3 + b^4
a^4 + b^4	= =	(a + b)² (a – b)² – 2a²b² aucune factorisation
a^4 – b^4	= = = =	(a² + b²) (a² – b²) (a² + b²) (a + b) (a – b) (a + b) (a^3 – a^2b + ab^2 – b^3 ) (a – b) (a^3 + a^2b + ab^2 + b^3 ) >>>
a^4 + 4b^4	= =	(a² + 2ab + 2b²)( a² – 2ab + 2b²) [(a + b)² + b²] [(a – b)² + b²]
a^4 – 4b^4	=	(a² + 2b²) (a² – 2b²)
a^4 + b^4 + (a + b)^4	=	2 (a² + ab + b²)^2
(a + 1)^3 (a – 1)	=	a^4 + 2a^3 – 2a – 1
(a – 1)^3 (a + 1)	=	a^4 – 2a^3 + 2a – 1
(a + b + c)^4	=	a^4 + b^4 + c^4 + 4a^3b + 4a^3c + 4b^3c + 6a²b²+ 6a²c²+ 6b²c² + 4ab^3 + 4ac^3 + 4bc^3 12ab²c + 12abc² + 12a²bc
(a + b)^4 + (a – b)^4	=	2a^4 + 12a²b² + 2b^4
(a + b)^4 – (a – b)^4	=	8ab (a² + b²)
(a + b)^4 (a – b)^4	=	a^8 + b^8 + 6a^4b^4 – 4a²b² (a^4 + b^4)
(a + b)^4 / (a – b)^4		rien d'intéressant
a^4 + a^2 + 1	=	(a² + a + 1) (a² – a + 1) Identité d'Argand >>>
a^4 + a^3 + a + 1	=	(a + 1)^2 (a² – a + 1)
a^4 – a^3 – a + 1	=	(a – 1)^2 (a² + a + 1)

Voir Identité de Sophie Germain

n^4 – 1	= = =	(n + 1) (n^3 – n^2 + n – 1) (n – 1) (n^3 + n^2 + n + 1) (n – 1) (n + 1) (n² + 1) >>>
n^4 – n = n (n^3 – 1)	=	n (n – 1) (n² + n + 1)
n^4 + n^2 + 1 =	= =	n^4 + 2n^2 + 1 − n^2 = (n^2 + 1)^2 − n^2 (n^2 + n + 1)(n^2− n + 1)
n^4 + 4	= =	(n^2 +2)^2 – 4n^2 (n^2 – 2n + 2n) (n^2 + 2n + 2)
n^4 + 4^n	=	(2^n + n^2)^2 – n^2 2^n+1 >>>
n^4 + 2n^3 – n^2 – 2n	=	(n – 1) n (n + 1) (n + 2) >>>

(n² + 3x + 1)²	= =	n (n + 1) (n + 2) (n + 3) + 1 Application n^4 + 6n^3 + 11n^2 + 6n + 1
(n² + 3x – 1)²	= =	(n – 1) n (n + 1) (n + 2) + 1 n^4 + 2n^3 – n^2 – 2n + 1
(n² + 3x – 1)²	= =	(n – 2) (n – 1) n (n + 1)) + 1 n^4 – 2n^3 – n^2 + 2n + 1
n(n+1)(n+2)(n+3) + 1	= =	n^4 + 6n^3 + 11n^2 + 6n + 1 (n^2 + 3n + 1)^2

Voir Produit de 4 nombres consécutifs +1 = carré

n^4 + n^2 + 1	=	(n² – n + 1) (n² + n + 1)
	=

Voir Application a la somme d'une suite

n⁴ + 4 n'est premier que pour n = 1,

seule valeur portant le premier facteur à 1.

n⁴ + 4ⁿ n'est premier que pour n = 1 Voir Démo

Identité de Sophie Germain

Identité de Fauquembergue

Identité des congruum

Factorisations inattendues (introduction de radicaux)

IDENTITÉS avec le 5^e degré
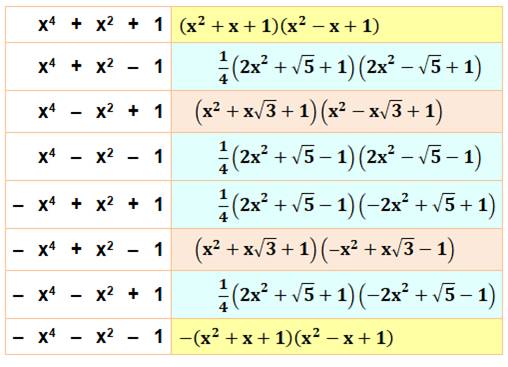
(a + b)^5	=	a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5
(a – b)^5	=	a^5 – 5a^4b + 10a^3b^2 – 10a^2b^3 + 5ab^4 – b^5
a^5 + b^5	=	(a + b) (a^4 – a^3b + a^2b^2 – ab^3 + b^4 )
a^5 – b^5	=	(a – b) (a^4 + a^3b + a^2b^2 + ab^3 + b^4 ) >>>
a^5 + 1	=	(a + 1) (a^4 – a^3 + a^2 – a + 1 )
a^5 – 1	=	(a – 1) (a^4 + a^3 + a^2 + a + 1 )

Autrement-dit (exemple)

=

(a + 1)^3 (a – 1)^2	=	a^5 + a^4 – 2a^3 – 2a^2 + a + 1
(a – 1)^3 (a + 1)^2	=	a^5 – a^4 – 2a^3 – 2a^2 + a – 1

n^5 – n	=	(n – 2) (n – 1) n (n + 1) (n + 2) + 5 (n – 1) n (n + 1) Voir Divisibilité par 30
n^5 – 5n^3 + 4n	=	(n – 2) (n – 1) n (n + 1) (n + 2) >>>
n^6– 1	=	(n+1) (n–1) (n^4+n^2+1)
n^7– n	=	(n+1) n (n–1) (n^4+n^2+1)

n^5 – n Les 6 seules possibilités

= = = = = =

(n^2 – n + 3) (n^3 + n^2 – 2n – 5) + 15 (n^2 + n + 3) (n^3 – n^2 – 2n + 5) – 15 (n^3 – 12n^2 + 89n – 408) (n^2 + 12n + 55) + 22 440 (n^3 + 12n^2 + 89n + 408) (n^2 – 12n + 55) – 22 440 (n^3 + 12n^2 – 233n – 7 320) (n^2 – 12n + 377) + 2 759 640 (n^3 – 12n^2 – 233n + 7 320) (n^2 + 12n + 377) – 2 759 640

IDENTITÉS de degré > 5
a^6 + b^6	=	(a² + b²) (a^4 – a^2b^2 + b^4)
a^6 – b^6	=	(a + b) (a – b) (a² + ab + b²) (a² – ab + b²)
a^7 + b^7	=	(a + b) (a^6 – ab^5 + a^2b^4 – a^3b^3 + a^4b^2 – a^5b + b^6)
a^7 – b^7	=	(a – b) (a^6 + ab^5 + a^2b^4 + a^3b^3 + a^4b^2 + a^5b + b^6) >>>
a^8 + b^8	=	aucune factorisation
a^8 – b^8	=	(a + b) (a – b) (a² + b²) (a^4 + b^4) >>>
a^9 + b^9	= = =	(a + b) ( a^8 – a^7b + a^6b^2 – ... + b^8) (a^3 + b^3) ( a^6 – a^3b^3 +b^6) (a + b) (a^2 – ab + b^2) ( a^6 – a^3b^3 +b^6)
a^9 – b^9	=	(a – b) (a^2 + ab + b^2) ( a^6 + a^3b^3 + b^6) >>>
a^10 + b^10	=	(a² + b²) (a^8 – a^6b^2 +a^4b^4 – a^2b^6 + b^8)
a^10 – b^10	=	(a + b) (a – b) (a^4 + a^3b + a²b² + ab^3 + b^4) (a^4 – a^3b + a²b² – ab^3 + b^4)
a^11 + b^11	=	(a + b) ( a^10 – a^9b + a^8b^2 – ... + b^10)
a^11 – b^11	=	(a – b) ( a^10 + a^9b + a^8b^2 + ... + b^10)
a^12 + b^12	=	(a^4 + b^4) (a^8 – a^4b^4 + b^8)
a^12 – b^12	=	(a + b) (a – b) (a² + b²) (a² + ab + b²) (a² – ab + b²) (a^4 – a²b² + b^4) Son calcul >>>

Voir Identités en aⁿ + bⁿ et applications / Identités en aⁿ - bⁿ et applications

Identités en n^k – n avec k impair

Notez les possibilités accrues pour k premier, confirmant le petit théorème de Fermat

Merci à Alain Fabo pour m'avoir proposé ces relations

BINÔME DE NEWTON

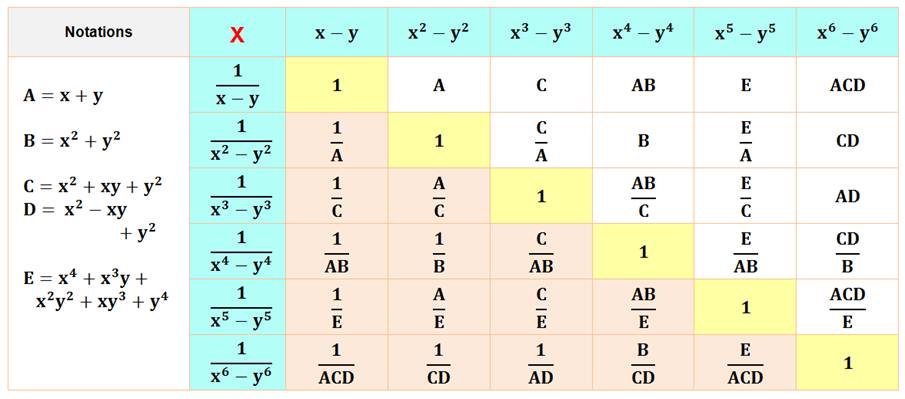
Il s'agit du développement de la somme a+ b à une certaine puissance. Les coefficients des termes sont les nombres du triangle de Pascal. Voir Cas où b = 1 Formulation générale Notation développée (coefficients à la française) Notation abrégée (coefficients à l'anglo-saxonne) Correspondance entre les notations Attention à l'inversion des indices. Ces nombres, les coefficients binomiaux, sont aussi la quantité de combinaisons de n éléments pris k à k. Le point d'exclamation est le symbole de factoriel.

Voir Fermat et Pascal / Newton / Combinaisons

(a – b)^n
La quantité de facteurs est égale à la quantité de diviseurs de l'exposant. Exemple avec 12 qui a six diviseurs (1, 2, 3, 4, 6, 12), il ya six facteurs. Calcul: 12 = 2^2 x 3^1, alors, on ajoute 1 aux exposants et on multiplie: (2 + 1) (1 + 1) = 6.

(a+b)^n

Voir Coefficients du binôme / Application à la caractérisation des unités / Binôme complexe

Identités en a^n et b^n
a^n – b^n	=	(a – b) (a^n–1 + a^n–2 b + ... + ab^n–2 + b^n–1)
a^2 – b^2 a^3 – b^3 a^4 – b^4 a^5 – b^5	= = = =	(a – b) (a + b) (a – b) (a^2 + ab + b^2) (a – b) (a^3 + a^2b + ab^2 + b^3) (a – b) (a^4 + a^3b + a^2b^2 + ab^3 + b^4)
a^7 – 1 (exemple)	=	(a – 1) (a^6 + a^5 + a^4 + a^3 + a^2 + a + 1) >>>
a^n – 1	=	(a – 1) (a^n–1 + a^n–2 + ... + a + 1)
a^2n+1 – 1	=	(a – 1) (a^2n + a^2n–1 + ... + a + 1)

a^n + b^n n impair	=	(a + b) (a^n–1 – a^n–2 b + ... – a b^n–2 + b^n–1)
a^2 + b^2 a^3 + b^3 a^4 + b^4 a^5 + b^5 a^7 + b^7	= = = = =	/ (a + b) (a^2 – ab + b^2) / (a + b) (a^4 – a^3b + a^2b^2 – ab^3 + b^4) (a + b) (a^6 – a^5b + a^4b^2 – a^3b^3 + a^2b^4 – ab^5 + b^6)

a^3 + 1	=	(a + 1) (a² – a + 1)
a^5 + 1	=	(a + 1) (a^4 – a^3 + a^2 – a + 1)
a^7 + 1	=	(a + 1) (a^6 – a^5 + a^4 – a^3 + a^2 – a + 1)
a^n + 1 n impair	=	(a + 1) (a^n–1 – a^n–2 + ... – a + 1)
a^2n+1 + 1	=	(a + 1) (a^2n – a^2n–1 + ... – a + 1)

Voir Divisibilité de ces formes / Impair / Formes en aⁿ +1 / Factorisation de bⁿ + 1 avec b impair

Merci à François Kany pour ses remarques

Sommes limitées & Sommes infinies pour x < 1

1 + x + x^2 + … x^n	=	(1 – x^n+1) / (1– x)
(1 – x) (1 + x + x^2 + …)	=	1 / (1–x)

Voir Sommes infinies

Divisions du type

Factorielles tronquées

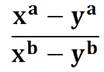
Voir Suite >>> (nombres de Stirling)

Suite	Autres identités importantes Degré 7 Identité de Ramanujan – Somme des cubes Quelques développements de Taylor Somme des entiers, des carrés, des inverses…
Voir	Application aux multiplications Applications à la résolution d'équations de degré > 2 Constantes Différences entre puissances Égalités dans les triangles Factorisation selon Fermat Identité de Lagrange Identités trigonométriques Isopérimètre Nombres cubains Pépites Somme Somme de carrés de nombres consécutifs Somme des entiers, des carrés… Tautochronie Théorèmes
Site	A Collection of Algebraic Identities – Tito Piezas A Collection of Algebraic Identities – Anthony L. Hart Sums of four or more Fourth Powers Aurifeuillian factor – Prime Wiki – Diverses factorisations de polynômes (utiles pour factoriser les nombres de Cunningham)
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/IdentAut.htm