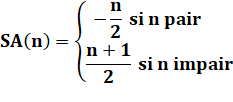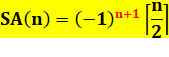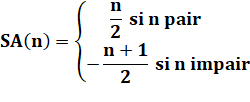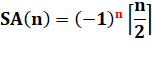|
|||||||||||||||||||||||||||||
![]()
|
Sommes alternées des entiers Somme des nombres entiers de
1 à n avec succession alternées de plus et de moins. En
fait, différence entre
nombres pairs et impairs. |
|
|
||
|
Je vérifie facilement que
jusqu'à 10: |
1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 – 10 = (1 – 2) + (3 – 4) + (5 – 6) + (7 – 8) + (9
– 10) = 5 x (– 1) = – 5 |
|
|
Jusqu'à 100: |
1 – 2 + 3 – 4 + 5 … – 100
= – 50 |
|
|
Et jusqu'à 2n: |
1 – 2 + 3 – 4 + 5 … – 2n
= – n |
|
|
Ci-contre, calcul classique avec deux
sommes "inverses" pour 2n = 100. Note: un calcul plus rapide consiste à former des
couples comme: Il y a 50 tels couples, soit un total de –50. |
Somme des impairs de 1 à 99 Si = 1 + 3 + 5 + 6 + 7 … + 97 + 99 2Si = 100 + 100 + … + 100 + 100 2Si = 100 x 50 = 5 000 Somme des pairs de 2 à 100 Sp = 2 + 4 + 6 + … + 98 + 100 Sp = 100 +
98 + … + 6 + 4
+ 2 2Sp = 102 + 102 + … + 102 + 102 2Sp = 102 x 50 = 5100 Somme alternée totale S = Si – Sp = ½ (5000 – 5100) =
– 50 |
|
|
|
||
|
Alternée:
Impairs – Pairs S = 1 – 2 + 3
– 4 + … + 2n – 1 – 2n S = 1 – 2 + 3
– 4 + … – 2n + 2n + 1 |
Voir Somme des pairs et des impairs
|
|
|
S(x= – 1 ) = 1 + 2x + 3x2 + 4x3+
… + n . xn+1 S = 1 – 2 + 3
– 4 + … + n . ( –1)n+1 Voir Valeur
plafond (crochets hauts) |
|
|
|
Alternée:
Pairs – Impairs S = –1 + 2 – 3
+ 4 – … – 2n – 1 + 2n S = –1 + 2 –
3 + 4 – … + 2n
– 2n + 1 |
|
|
|
S = –1 + 2 – 3 +
4 – … + n . ( –1)n = – S(x= – 1 ) |
|
|
|
Cas pathologiques S = 1 – 1 + 1
– 1 … S = 1 + 2 + 3 + … |
S = {0, ½, 1} ?
S = - 1/12 ???
|
|
|
Série infinie 1 – 2 + 3 – 4 + 5 – ... – 2n + … |
= 1/4 |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()