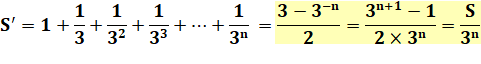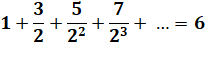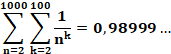|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES avec des PUISSANCES SUCCESSIVES Les
sommes classiques des nombres successifs ont déjà
été vues:
Cette
page est consacrée à des sommes qui font intervenir un même motif impliquant
des puissances successives. Ne pas confondre:
|
Voir Nombres
consécutifs / Suites géométriques
|
|
||
|
Formule générale
Cas des puissances de 2
|
Exemples 40 + 41 + 42 + 43 + 44
= 1 + 4 + 16 + 64 + 256 = 341 1 + 10 + 100 + 1 000 = 1 111 1 + 2 + 4 + 8 + 16 + …+ 1 024 = 2 048 – 1 = 2 047 |
|
|
Valeur de a en horizontal et de n
en vertical
Nombres de ce tableau jusqu'à 1111.
Ils sont 37. 1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 15, 21, 31, 40, 43, 57, 63, 73,
85, 91, 111, 121, 127, 156, 255, 259, 341, 364, 400, 511, 585, 781, 820,
1023, 1093, 1111. |
||
|
|
||
|
Formules générales Elles
découlent directement de la division indiquée en rouge, elle-même faisant
l'objet d'une identité remarquable. Ces identités
remarquables se retrouvent en numération
où n représente la base ou encore pour caractériser certains nombres
brésiliens (repdigits). Cas particulier où n = 2 Notons que la
sommes des puissances successives de 2
est égale à la puissance suivante décrémentée de un. |
Suites géométriques de raisons a et
1/a
Ex: 1 + 5 + 5² = 31 = (53 – 1) / (5 – 1) ) = 124 / 4 = 31 1 + 1/5 + 1/5² = 1 + 0,2 +
0,04 = 1,24 = 124 /(4 x 5²) = 1,24 Suites géométriques de raisons 2 et
1/2
Ex: 1 + 2 + 2² = 7 = 23 – 1 = 7 1 + 1/2 + 1/4 = 1,75 = 7 / 2² = 1,75 |
|
Voir Suites géométriques
/ Nombres
décimaux et périodiques
Merci à Frank J. pour sa
contribution
|
|
||
|
Avec puissances de 2 Exemple |
n = 5 1x4 + 3x8 + 5x16 + 7x32 +9x64 = 908 = 32(40-12) + 12 |
|
|
Avec inverse des puissances de 2 Exemples |
Voir DicoNombre
6 n = 5 => S = 5,53… n = 10 => S = 5,97… n = 20 => S = 5,999957… |
|
|
|
||
|
Avec puissances de 3 Exemples |
Suite géométrique de raison 3
n = 5 => S = 364 |
|
|
Avec inverse des puissances de 3 Exemples Somme infinie |
Suite géométrique de raison 1/3
n = 5 => S' = 364 / 243 =
1,4979…
|
|
|
Sommes infinies avec numérateur |
Voir DicoNombre
2,25
Voir DicoNombre
0,75
Voir DicoNombre
6 |
|
|
Produit Notations Exemples |
n = 1 => P = 40/27 = 1,481 481 … n = 3 => P = 1,499999965… n = 5 => P = 1,5 à 10
-31 près. Ce
produit tend vers 1,5 pour n infini. |
|
|
|
||
|
Avec puissances de 4 Exemples |
Suite géométrique de raison 4
n = 3 => S = 85 n = 10 => S = 1 398 101 |
|
|
Avec inverse des puissances de 4 Exemples Somme infinie |
Suite géométrique de raison 1/4
n = 3 => S' = 85 / 64 =
1,328125 n = 10 => S' = 1 398 101 / 1 048 576 = 1,333333015…
|
|
Voir Somme
des puissances quatrièmes
|
|
||
|
Avec puissances de 5 |
|
|
|
Avec puissances de
A >1 |
Somme des puissances n d'un entier
A
Somme des puissances n de l'inverse
d'un entier A
Exemple avec l'inverse de A = 10
|
|
|
Puissances de 5 et numérateur Exemples |
n = 5 => S'n =
39 / 25 = 1,56
|
|
|
|
||
|
Entier, carrés et cubes Exemple |
n= 3 => 3/2 + 14/6 + 39/12 = 85/12 = 7,08333… = 1 + 2 + 3 + 1/2 +
1/3 + 1/4 = 85/12 |
|
|
Exemple Calcul Voir Identités avec le quatrième
degré |
n= 3 =>
|
|
Voir Carrés
et inverses
|
Calcul simple des
sommes des puissances successives de 9 (par factorisation)
Deux méthodes voisines
pour le calcul des six puissances successives (hors le 1 = 90)
Liste des 20 premières
sommes des puissances de 9 1, 10, 91,
820, 7381, 66430, 597871, 5380840,
48427561, 435848050, 3922632451, 35303692060, 317733228541, 2859599056870,
25736391511831, 231627523606480, 2084647712458321, 18761829412124890,
168856464709124011, 1519708182382116100, … Notez l'alternance 0, 1
pour les unités explicable par le
calcul par factorisation. Ce sont les nombres de la forme (9n
– 1)/8 qui sont aussi les nombres
triangulaires différences
de carrés; aussi les repunits
(1, 11, 111, …) en base
9 |
|
Voir Brève 58-1147 / Somme
des mêmes chiffres
![]()
|
|
||||
|
Fraction Exemple |
|
|||
|
Puissances 2 et 3 Exemple |
Voir Recherche de
formule
|
|||
|
Puissances 2 et 4 Exemple |
|
|||
|
Puissance et infinis |
|
Voir Formule de
Goldbach |
||
|
Puissances et factorielles |
La énième différence finie des puissances énièmes est égale à
factorielle n.
|
Voir Explications et démonstration |
||
|
inverses de 2 |
|
|
||
|
|
||
|
La somme des inverses de toutes les
puissances parfaites, y compris les doublons, vaut 1. Notez bien le départ
des indices: n = 2 et k = 2.
En effet:
Note 1: voir le tableau ci-dessous pour visualiser
la légitimité de la mise en facteur commun de 1/n². Note 2: les fractions finales, impliquant des
nombres consécutifs, s'éliminent deux à deux:
Seule la première (1) et la dernière (qui
tend vers 0) subsistent. Exemple de valeurs numériques Jusqu'à n = k = 10
Jusqu'à n = k = 100
Son calcul avec Maple
La convergence vers 1 est très lente: avec
n = k = 1000, on a 0,9990… Exemple de début de calcul
|
||
|
Cas des puissances (et non
des inverses) Pour
information la somme des puissances (les mêmes, mais en partant de 1 et non
de 2) donne: 11
+ 12 + 21 + 22 = 8; 11
+ 12 + 13 + 21 + 22 + 23
+ 31 + 32 + 33 = 56. Suite
sur le tableau => Notez la curiosité
avec des couples de 6 au dixième rang. S
= 16676686632 = 1,667668663 1010 |
|
|
Immense merci à Claude
M. pour sa contribution qui a conduit à mettre à jour cette
page
![]()
|
Retour |
|
|
|
|
|
Table |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomPuiss.htm |
![]()