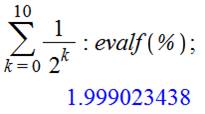|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
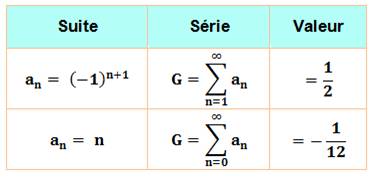
SÉRIES en: 1 – 1 + 1 – 1 + … et aussi: 1 +
2 + 3 + 4 + … Somme alternées et convergences ? |
|
|
Il
existe trois types de séries:
Nous
nous intéressons au dernier cas pour lequel une extension de la notion de
convergence a été imaginée: la somme de Cesaro. |
Vrai ou faux ?
Vrai sous certaines conditions ! |
Voir DicoMot Maths – Suites et Séries
|
Les
séries divergentes sont une invention du diable
et c’est une honte qu’on ose fonder sur elles la moindre démonstration. On
peut tirer d’elles tout ce qu’on veut quand on les emploie et ce sont elles
qui ont produit tant d’échecs et tant de paradoxes. (…) Mes amis, voici
quelque chose dont il faut se moquer. Abel – 1826 |
Voir Pensées & humour
|
|
|||||||||||||
|
Trois résultats pour une série.
En fait, cette série n'est pas
convergente, c'est tout! La somme 3 s'obtient également en
appliquant la formule en bas à gauche du tableau ci-dessus. Historique Luigi Guido Grandi (1671 – 1742)
analyse la série qui porte son nom et en tire des conclusions théologiques
controversées. Wilhelm Leibniz (1646-1716) ayant
trouvé S = 0 et S = 1 et constatant que la probabilité de chaque valeur
devait être égale, avait conclu que S = ½, c'est-à-dire la valeur moyenne.
|
|||||||||||||
|
|
|
|
Euler
avec sa méthode, sans se soucier des questions de convergence, trouve une formule générale qui lui permet
de calculer des suites infinies en donnant une valeur à la variable.
|
|
Voir Développement en série entière de la fonction
1 / (1 + x)
Produit infini de puissances
de 2 / Brève
895 / Nombres p-adiques
|
|
|
|
En
reprenant la suite qui rend fou et en lui affectant la valeur moyenne de ½,
nous calculons la suite S3 égale à la somme des entiers. Paradoxe: la somme des entiers vaut –
1/12 = – 0,08333… Premier calcul de Ramanujan Srinivasa
Ramanujan
(1887-1920) fait ce calcul étrange:
Évidemment
le loup est dans la valeur de la suite initiale. Sa valeur moyenne égale à ½
n'est pas légitime. Deuxième calcul de Ramanujan –
Sommation de Ramanujan Il
utilise le calcul d'une suite alternée selon la méthode d'Euler, exposée
ci-dessus.
Cette
fois, pas d'hypothèse, alors … ? Autres bizarreries de Ramanujan Somme au
sens de Ramanujan parfois accompagnée d'un symbole
|
|
Voir Brève
894
Merci à Frédéric D. pour
ses remarques
|
|
||
|
Somme de Cesarlo Ernesto Cesaro (1859-1906) définit une moyenne pour donner une
valeur à ce type de série sans convergence. |
On calcule toutes les sommes
partielles avec les k premiers termes (Sk) et on en prend la moyenne
arithmétique à chaque fois.
|
|
|
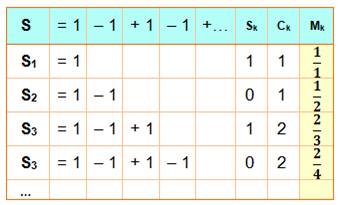
Dans le cas de la suite de Grandi Le
tableau montre le principe du calcul. Les moyennes successives sont: La limite
est égale à 1/2 |
|
|
|
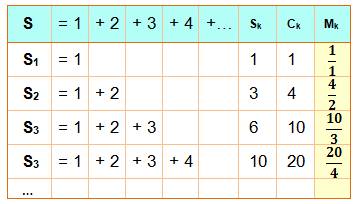
Dans le cas de la suite de
Ramanujan Cette
fois, la suite est divergente. Pas de limite à la somme au sens de Cesaro. |
|
|
Voir Notions de somme classique et
avancée
|
Pas
question de dire que ces suites ont une véritable valeur. Pour Cesaro et avec
sa somme (on dit plutôt "sommation",
il s'agit d'attribuer une grandeur (une mesure, une étiquette)) à la suite
lorsque c'est possible. Cette manière de faire n'est pas toujours couronnée
de succès. C'est le cas notamment avec la suite des nombres entiers. Pour
étendre la notion de convergence d'autres méthodes de sommation ont également
été imaginées. |
Anglais
|
The Cesàro
sum is defined as the limit of the arithmetic mean of the partial sums
of the series. The Cesaro
sum of an infinite series is the limit of the arithmetic mean
(average) of the first n partial sums of the series, as n goes to infinity. One can readily verify that the
Cesaro sum of 1-1+1-1+... is 1/2, which is a bit intuitive to expect. On the
other hand the series 1+2+3+... is not even summable using Cesaro method; it
again diverges to infinity. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()