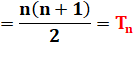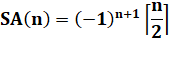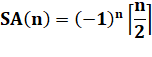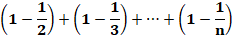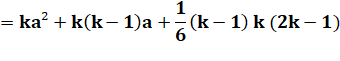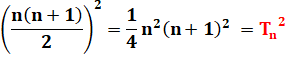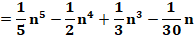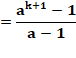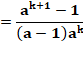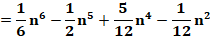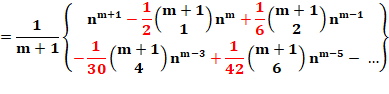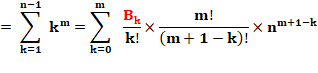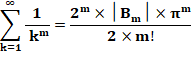|
||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES de NOMBRES Index et formules de base Ne pas confondre
|
|
|
||
|
Général |
– Méthode de Gauss enfant
|
|
|
Nombres successifs à la même puissance |
Entiers Puissances Autres |
||||||||||||||||||||||||||||||||||||
|
Puissances successives |
|||||||||||||||||||||||||||||||||||||
|
Démonstrations |
|
||||||
|
Tables |
|
|
|
||||
|
1 + 2 + 3
+ … + n |
|
|||
|
Pairs |
2 + 4 + 6
+ … + 2n |
= n (n + 1) = n² + n = 2Tn |
||
|
Impairs |
1 + 3 + 5
+ … + (2n – 1) |
= n2 |
||
|
Symétrique |
1 + 2 + …n
… + 2 + 1 |
= n² |
||
Suite Sommes
des entiers
|
Impairs - pairs |
S = 1 – 2 + 3 – 4 + …
+ n . ( –1)n+1 |
|
|
|
Pairs - Impairs |
S = –1 + 2 – 3 + 4 – … + n . ( –1)n |
|
Suite Sommes alternées des entiers
|
Thue-Morse |
1² – 2² – 3² + 4² – 5² +
6² + 7² – 8² 1² + 4² +
6² + 7² = 2² + 3² + 5² + 8² = 102 |
= 0 |
|
Pronique |
1x2 + 2x3
+ 3x4 + 4x5 + … + n(n+1) |
= 1/3 n(n+1)(n+2) |
|
|
Produit de trois |
1x2x3 +
2x3x4 … + n(n+1)(n+2) |
= 1/4
n(n+1)(n+2)(n+3) |
|
|
Puissances |
1/1k +
1/2k +1/3k +1/4k +… |
= |
|
|
1/2k |
1 + 1/2 + 1/4 + 1/
8 + 1/16 |
= 2 |
|
Sommes des inverses –
Formulaire |
|
|
|||
|
Inverses Série harmonique |
|
|
|||
|
Inverses alternés Série semi-harmonique |
|
= ln2 = 0,6931… |
|||
|
Inverses opposés
(somme) |
|
n – Sh
|
|||
|
Inverses opposés
(produit) |
|
|
|||
|
|
|
||||
Suite Autres sommes
d'inverses et développements
|
Sommes des puissances –
Formulaire |
|
|||
|
1² + 2² +
… + n² |
|
|||
|
1² + 2² +
… + (n-1)² |
|
|||
|
À partir de a avec k termes |
a² + (a +
1)² + … + (a + k – 1)² |
|
||
Suite Somme des
carrés, des inverses des carrés …
|
13
+ 23 + … + n3 |
|
||
|
Bicarrés |
14
+ 24 + … + (n-1)4 |
|
|
|
Puissances d'un nombre |
1 + a + a2
+…+ ak |
|
|
|
Puissances de l'inverse |
1 + 1/a +
1/a2 +…+ 1/ak |
|
|
|
Puissance 5 |
15
+ 25 + … + (n-1)5 |
|
|
|
Puissance quelconque |
1m
+ 2m + … + (n-1)m |
|
|
|
Puissance des inverses |
|
Suite par Type de nombre
|
|
|
||||
|
|
1 2 3 4 5 6 7 8 9 10 … |
S ligne n = n/2 (n²+1) |
|||
|
|
Pyramide impaire |
1 3 5 7 9 11 13 15 17
19 … |
S ligne n = n3 |
||
Voir Suite et
démo / Pyramides et carrés
|
|
|
||||
|
|
1 2 3 4 5 6 7 8 9 10 … |
S ligne n = n/2 (n²+1) |
|||
|
|
Pyramide impaire |
1 3 5 7 9 11 13 15 17
19 … |
S ligne n = n3 |
||
Voir Suite et
démo / Pyramides et carrés
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()