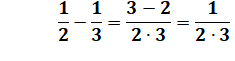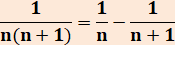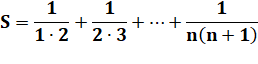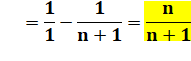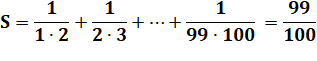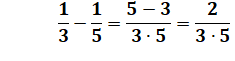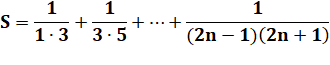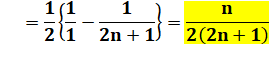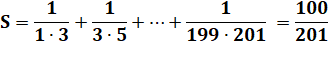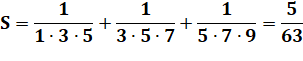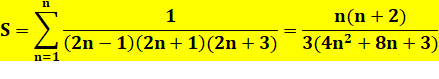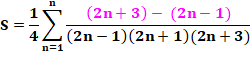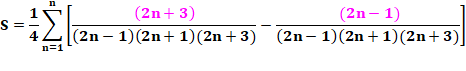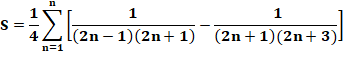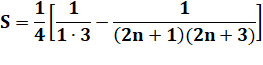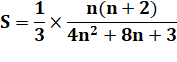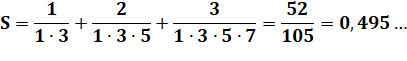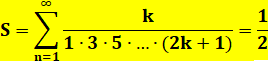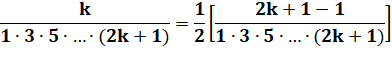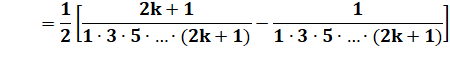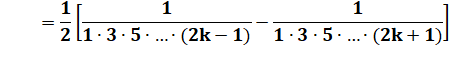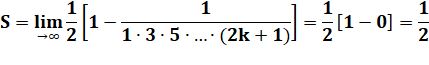|
Édition du: 02/11/2021 |
|
INDEX |
Sommes d'inverses |
|||
![]()
|
Sommes d'inverses de produits (SIP) Les
démonstrations pour aboutir à une formulation de telles sommes font appel à
la somme télescopique: les
termes s'acculent en cascade pour ne conserver que le premier et le dernier. |
||
|
|
Sommaire de cette page >>>
SIP avec deux entiers >>>
SIP avec deux impairs >>>
SIP avec trois impairs |
Débutants Glossaire |
|
Exemple:
calculez (avec astuces !)
On remarque que, par exemple:
En appliquant à toutes les fractions:
|
Propriété
Formule
générale
Exemple
|
|
Voir Brève
774
|
Exemple:
calculez (avec astuces !)
On remarque que, par exemple:
En appliquant à toutes les fractions:
|
Propriété
Formule
générale
Exemple
|
|
Voir Brève
775
|
Exemple |
|
|
|
Formule |
|
|
|
Démonstration Mise en évidence d'un 4 (astuce !) |
|
|
|
Mise en évidence de deux nombres du dénominateur |
|
|
|
Fractions séparées |
|
|
|
Simplification |
|
|
|
Somme télescopique |
|
|
|
Résultat |
|
|
|
Simplification |
|
|
|
SIP avec k
impairs successifs |
||
|
Exemple |
|
|
|
Formule |
|
|
|
Préparation du numérateur |
|
|
|
Séparation en deux termes du sommant |
|
|
|
Simplification du premier terme |
|
|
|
Somme télescopique: premier et dernier termes |
|
|
|
Passage à la limite pour l'infini |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |