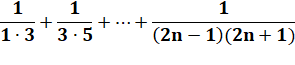|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES D'INVERSES de toute nature Exploration générale. |
|
Sommes des inverses –
Formulaire |
|
|
|||
|
Inverses Série harmonique |
|
|
|||
|
Inverses alternés Série semi-harmonique |
|
= ln2 = 0,6931… |
|||
|
Inverses opposés
(somme) |
|
n – Sh
|
|||
|
Inverses opposés
(produit) |
|
|
|||
|
|
|
||||
|
Produits deux impairs |
|
|
|||
|
Produits trois impairs |
|
|
|||
|
|
Produits combinés entiers et impairs |
|
= 2 – 2 ln2 |
||
|
Symétrique centrée sur n |
1 + 2 +… + (n–1) + n + (n–1) +…+ 2 + 1 |
= n² |
|||
|
Produits de deux entiers |
|
|
|||
|
Triangulaire |
|
= 2 |
|||
|
Inverse de 2 |
|
|
|
|
Inverse de 2, infini |
|
= 2 |
|
|
Inverse de n |
SG de
raison 1/n |
|
|
|
Inverse de n, infini |
|
Voir Nombres périodiques |
|
Impair et Inverse de 2 |
|
= 6 |
|
|
|
Inverse de 3 |
(1+1/3)
(1+1/32) (1+1/33) (1+1/34) … (1+1/32n) |
=
3/2 (1 - 3-2n+1) |
|
|
En 5 |
1 + 2/5
+ 3/5² + 4/53 … |
25/16(1-1/5n)
- 1/4 n(1/5n-1) |
|
|
En 5 |
5/13 +
55/13² + 555/133 + 5555/134 + … |
=
65/36 |
Voir Inverses des
carrés / Autres suites d'inverses
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/IdentInv.htm |
![]()